1944年,Nadolschi研究刚体运动时引入一个混沌系统其特点是方程右端含有3个非线性项,该系统称为Nadolschi混沌系统。混沌系统是指在一个确定性系统中,存在着貌似随机的不规则运动,其行为表现为不确定性、不可重复、不可预测,这就是混沌现象。混沌是非线性动力系统的固有特性,是非线性系统普遍存在的现象。
表示方法一类混沌系统(1):
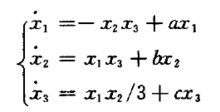
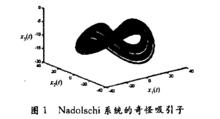
当参数取值为a=5,b=-10,c=-3.8,初值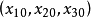 =(-12,5,-4)时,该系统存在图1所示的奇怪吸引子,即为混沌系统,通常被称为Nadolschi混沌系统。
=(-12,5,-4)时,该系统存在图1所示的奇怪吸引子,即为混沌系统,通常被称为Nadolschi混沌系统。
将式(2)作为响应系统,取式(1)为驱动系统,设计一个稳定的控制器使上述系统实现自相似结构渐近同步。式(2)为:
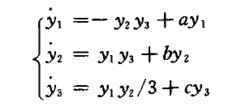
其中参数取为a=5,b=-10,C=-3.8,初值取为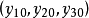 =(-7,8,-11)。
=(-7,8,-11)。
在混沌同步中,用到的反馈方法主要有参数反馈和状态变量反馈两种。参数反馈是指利用反馈的误差信号去调整系统的参数,使两个混沌系统实现同步化。状态变量反馈指的是反馈的信号直接加到响应系统的状态变量上去,不改变系统的参数。状态变量反馈可以有多种形式,可以是线性的,也可以是非线性的。这里,采用线性状态变量反馈方法设计同步控制器1。
性状态反馈控制器设计引入状态反馈控制的响应系统可以表示为式(3):
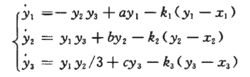
由驱动系统和响应系统构成的误差系统可以表示为式(4):
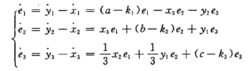
显然,误差系统的原点(e1=e2=e3=0)是该系统的平衡点,因此,可以选取合适的k1,k2和k3的值,使误差系统在零平衡点处渐近稳定,即混沌系统达到自相似结构同步。
Nadolschi混沌系统同步的充分条件对于式(4)所示的误差系统,当下列条件满足时,误差系统是渐近稳定的,即驱动系统和响应系统达到渐近同步:
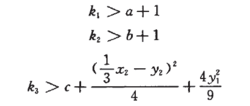
利用T-S模糊模型可以对Nadolschi混沌系统进行建模,并设计一个稳定的控制器使上述系统渐近稳定在零不动点上2。
首先提出三点假设:
(1)由于混沌系统的有界性,可以定义系统状态轨迹的研究范围为:
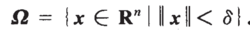
(2)混沌系统用T-S模糊模型表示时,其规则的前件变量独立于模型的控制输入。
(3)可以对混沌系统的每一个状态施加反馈控制,用T-S模糊模型表示时,体现为可以用PDC方法进行有效控制。
在以上3条假设成立的前提下,当参数已知时,可以利用T-S模型表示Nadolschi混沌系统。Nadolschi混沌系统可以用包含以下4条规则的模糊模型表示:
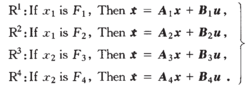
其中
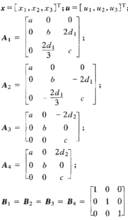
模糊集合Fi(i=1,2,3,4)的隶属度函数分别为
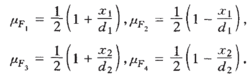




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国