[科普中国]-劳伦兹混沌系统

基本概念

1963年，Lorenz发现了第一个混沌吸引子——Lorenz系统，从此揭开了混沌研究的序幕。人们不断发现新的混沌奇异性，不断地加深与统一对混沌的理解。混沌系统是指在一个确定性系统中，存在着貌似随机的不规则运动，其行为表现为不确定性、不可重复、不可预测，这就是混沌现象。混沌是非线性动力系统的固有特性，是非线性系统普遍存在的现象。

模型Lorenz系统是数值试验中最早发现的呈现混沌运动的耗散系统，其状态方程为：

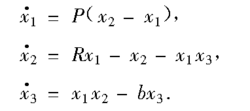
在a=10，b=8/3，c=28时呈现混沌态。该系统的一个简单物理实现是流体在下方加热上方冷却的热对流管中的环流，此时，x1是流体速度，x2和x3分别为水平和垂直的温度差，P与流体的Prandtl数成比例，b是与空间相关的常数，R与流体的Rayleigh数成比例1。

Lorenz系统的参数辨识自从1963年以来，对著名Lorenz系统的混沌行为已有系统研究随着混沌控制问题引起人们注意，控制Lorenz系统的混沌也有一系列工作。然而现有的工作，大多数控制方法均是在系统参数已知的情况下给出的；对于系统中存在未知参数时的情况较少被涉及。现存的很多控制方法，在参数未知的情况下不再适用。系统中未知参数的存在，为系统控制方法的设计增加了难度2。

下面是一种辨识系统局部参数的方法，其特点是：将未知参数作为系统的未知状态来处理，从而将辨识参数问题转化为未知状态的观测辨识问题。通过状态观测器的设计，来解决系统参数的辨识问题。

当系统参数P，R为已知参数，而b为未知参数时，在实际中需要得到未知参数b的值。然而，在很多情况下，未知参数的动态信息很难被得知，因此假定

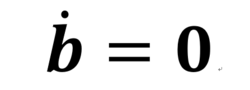
对于未知的参数b，把它作为状态变量，则可得到一增广的系统状态变量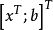更进一步，假设系统式中的所有状态均可得到，只需辨识未知的参数。

给出如下观测器：

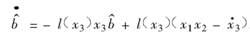
定义一个辅助变量

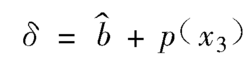
且令

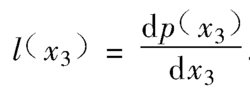
综合上面方程得到：

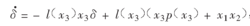
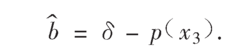
称上面两式组成的观测器为未知参数辨识观测器，其中p(x3)为被设计的函数。

动力系统辨识问题是动力学研究的逆问题，它利用系统在试验和运行中测得的输入输出数据，采用系统辨识技术，建立反映系统本质特性的数学模型，并辨识出模型中的待定参数。一般情况下，系统的动力学方程是已知的，需要辨识的只是动力学方程中的某些待定参数，诸如系统的模态参数或刚度，阻尼等结构物理参数，这属于典型的“灰箱问题”。

Lorenz系统和陈氏混沌系统1999年，美国休斯顿大学陈关荣教授发现了一个新的混沌吸引子——Chen系统，即陈氏混沌系统，它与Lorenz系统类似，但不拓扑等价而且更复杂。

Lorenz系统和陈氏混沌系统分别属于两个相反的类：

Lorenz系统满足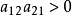，而陈氏混沌系统却满足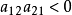，在这种意义下，他们是对偶的两个动力系统。由于陈氏混沌系统比Lorenz系统具有更复杂的拓扑结构和动力学行为，这一方面使得它在信息加密和保密通信等领域有着更广阔的应用前景，另一方面使得陈氏混沌系统很难控制，许多对Lorenz系统轻而易举的控制方法对陈氏混沌系统却不太理想甚至无效。尽管如此，目前对该系统的控制已有不少有效的控制方法，如：逆最优控制、识别控制、数字控制、模糊控制、脉冲控制、自适应控制等，随着研究的不断深入，在实际应用中必然要追求实施控制的有效性、代价大小和难易程度。