[科普中国]-准随机数- · 科普中国网

概念

准随机数发生器（QRNG）产生高度均匀的单位超立方体样本。 QRNG最小化生成点的分布与超立方体的统一分区的每个子立方体中具有相等比例点的分布之间的差异。因此，QRNG系统地填充所产生的准随机序列的任何初始段中的“空穴”。

与普通伪随机数生成方法中描述的伪随机序列不同，准随机序列在许多随机性的统计检验中失败了。然而，近乎真实的随机性并不是他们的目标。准随机序列寻求均匀填充空间，并以这样的方式进行，使得初始段近似该行为直到指定的密度。1

QRNG应用

（1）准蒙特卡罗（QMC）整合。

蒙特卡罗技术经常用于评估困难的多维积分，而无需封闭形式的解决方案。 QMC使用准随机序列来改善这些技术的收敛性质。

（2）空间填充实验设计。

在许多实验设置中，在每个因素设置下进行测量是昂贵的或不可行的。准随机序列为设计空间提供了有效、均匀的采样。

（3）全局优化。

优化算法通常在初始值附近找到局部最优值。通过使用初始值的准随机序列，搜索全局最优值对所有局部最小值的吸引盆地进行均匀采样。

准随机点集

统计和机器学习Toolbox™中有生成准随机序列的函数：

（1）哈尔顿序列。

由haltonset功能产生。这些序列使用不同的基数来形成每个维度中单位间隔的相继更好的均匀分区。

（2）Sobol序列。

由sobolset功能产生。这些序列使用2的基数来形成相继更精细的单位间隔的均匀分区，然后重新排列每个维度中的坐标。

（3）拉丁超立方体序列。

由lhsdesign功能制作。尽管在最小化差异的意义上不是准随机的，但是这些序列仍然产生在实验设计中有用的稀疏均匀样本。

准随机序列是从正整数到单位超立方体的函数。为了在应用中有用，必须生成序列的初始点集。点集是大小为n-by-d的矩阵，其中n是点的数量，d是被采样的超立方体的维度。函数haltonset和sobolset构造具有指定准随机序列属性的点集。点集的初始段由qrandset类（haltonset类和sobolset类的父类）的net方法生成，但可以使用括号索引更一般地生成和访问点。

由于产生准随机序列的方式，它们可能包含不期望的相关性，特别是在其初始段中，特别是在较高维度。为了解决这个问题，准随机点集经常跳过，跳过或扰乱序列中的值。 haltonset和sobolset函数允许您指定准随机序列的跳过和跳跃属性，而qrandset类的加扰方法允许您应用各种加扰技术。加扰减少了相关性，同时也提高了均匀性。

生成准随机点集

下面例子显示了如何在MATLAB中尝试使用haltonset来构建一个2-D Halton准随机点集。

创建一个haltonset对象p，它跳过序列的前1000个值，然后保留每101个点。

rng default % For reproducibilityp = haltonset(2,'Skip',1e3,'Leap',1e2)

p =

Halton point set in 2 dimensions (89180190640991 points)

Properties:

Skip : 1000

Leap : 100

ScrambleMethod : none

对象p封装指定的准随机序列的属性。点集是有限的，其长度由跳过和跳跃属性确定，并且由点集索引的大小限制。

使用加扰来运用反向加扰。

p = scramble(p,'RR2')

p =

Halton point set in 2 dimensions (89180190640991 points)

Properties:

Skip : 1000

Leap : 100

ScrambleMethod : RR2

使用网络生成前500个点。

X0 = net(p,500);

等效于

X0 = p(1:500,:);

点集X0的值不会生成并存储在内存中，直到使用网络或括号索引访问p。

为了诠释准随机数的性质，用X0创建二维的散点图。

scatter(X0(:,1),X0(:,2),5,'r')axis squaretitle('{\bf Quasi-Random Scatter}')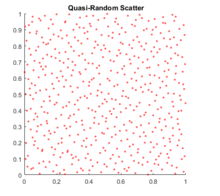

将其与由rand函数生成的均匀伪随机数的散点进行比较。

X = rand(500,2);scatter(X(:,1),X(:,2),5,'b')axis squaretitle('{\bf Uniform Random Scatter}')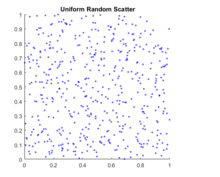

准随机散射看起来更均匀，避免了伪随机散射中的聚集。

在统计意义上，准随机数太均匀，不能通过传统的随机测试。例如，由kstest执行的Kolmogorov-Smirnov测试用于评估点集是否具有均匀的随机分布。在统一的伪随机样本（如rand所产生的样本）上重复执行时，测试产生均匀的p值分布。

nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests x = rand(sampSize,1); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval;endhistogram(PVALS,100)h = findobj(gca,'Type','patch');xlabel('{\it p}-values')ylabel('Number of Tests')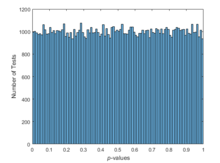

当在均匀的准随机样本上重复执行测试时，结果是完全不同的。

p = haltonset(1,'Skip',1e3,'Leap',1e2);p = scramble(p,'RR2');nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests x = p(test:test+(sampSize-1),:); [h,pval] = kstest(x,[x,x]); PVALS(test) = pval;endhistogram(PVALS,100)xlabel('{\it p}-values')ylabel('Number of Tests')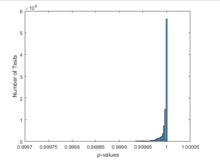

　　小的p值引起了数据均匀分布的零假设的质疑。如果这个假设是真实的，那么约有5%的p值预计会低于0.05。

准随机流

由qrandstream函数产生的准随机流用于生成顺序准随机输出，而不是特定大小的点集。如pseudoRNGS，当客户端应用程序需要可以间歇访问的无限大小的准随机数的来源时。当构建流时，设置准随机流的属性，例如其类型（Halton或Sobol）、维度、跳过、跳跃和加扰。

在实现中，准随机流本质上是非常大的准随机点集，尽管它们被不同地访问。准随机流的状态是要从流中获取的下一个点的标量索引。使用qrandstream类的qrand方法从当前状态开始从流中生成点。使用reset方法将状态重置为1与点集不同，流不支持括号索引。

生成准随机流

使用haltonset创建准随机点集p，然后将索引重复增加到点集测试中以生成不同的样本。

通过使用qrandstream基于点集p构造准随机流q并使流处理到索引的增量来获得相同的结果。

p = haltonset(1,'Skip',1e3,'Leap',1e2);p = scramble(p,'RR2');q = qrandstream(p);nTests = 1e5;sampSize = 50;PVALS = zeros(nTests,1);for test = 1:nTests X = qrand(q,sampSize); [h,pval] = kstest(X,[X,X]); PVALS(test) = pval;end