[科普中国]-陈氏混沌系统

1999年，美国休斯顿大学陈关荣教授发现了一个新的混沌吸引子——Chen系统，即陈氏混沌系统，它与Lorenz系统类似，但不拓扑等价而且更复杂。混沌系统是指在一个确定性系统中，存在着貌似随机的不规则运动，其行为表现为不确定性、不可重复、不可预测，这就是混沌现象。混沌是非线性动力系统的固有特性，是非线性系统普遍存在的现象。

1999年，陈关荣等人发现了一个与Lorenz混沌系统相类似但拓扑不等价的混沌吸引子，该系统描述如下（受控系统（1））：

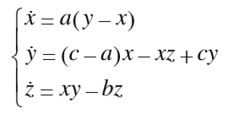
陈氏混沌系统（Chen）为典型的混沌系统，当a=35，b=3，c=28时，系统呈现混沌状态1。陈氏混沌吸引子如图所示：

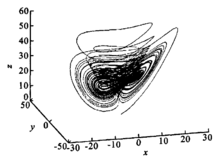
将各状态变量看作相位连续、包络随机变化的谐和信号，系统的特征频率定义为信号相位的平均变化率，即

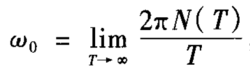
其中N为时间T内信号的波峰或波谷数目。对于陈氏系统可计算其特征频率为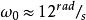 ，由于参数c的变化对系统行为具有较大影响，可设计参数激励非反馈控制系统如下：

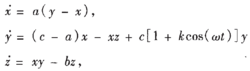
其中k是唯一的待定控制参数，激励信号频率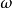 远大于系统特征频率 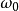，通过调节参数k使陈氏混沌系统稳定于周期状态或平衡点。

当a=35，b=3，c=28时，系统呈现混沌状态。此时数学模型为

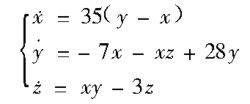
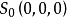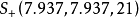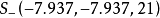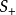此时系统处于混沌状态，有三个平衡点 ， ， 。 是鞍点， 和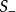 是不稳定焦点，对系统进行数值仿真出现混沌图形，轨线围绕两个不稳定焦点 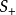和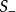 随机跳动，呈双螺旋状，如下图所示：

构造线性反馈控制器，控制陈氏混沌系统到达平衡点S=(x,y,z)，作坐标平移变换，令

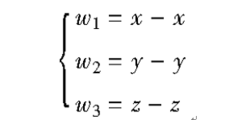
则受控系统（2）为：

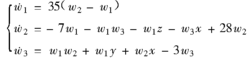
将线性反馈控制器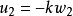 加到上述系统的第二个方程上，则受控系统（3）为

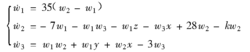
此时状态W指数稳定于点W0(0，0，0)，亦即原系统可按指数全局稳定于平衡点S=(x,y,z)。

对系统（2）的第二、第三个方程分别使用控制扰动：

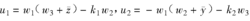
则受控系统（4）为：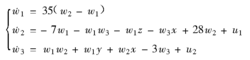

显然受控系统（4）与系统（2）有相同的不动点W0(0，0，0)，据Lyapunove稳定性原理，系统（2）能被控制到其平衡点，即原系统（1）能被控制到它的三个平衡点2。

假定响应系统具有3个未知不确定参数，同样假定系统式（1）为驱动系统，可以构建相应地响应系统（6）如下：

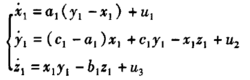
式中，u1，u2，u3为要设计的控制器。

由（6）减去（1）可得：

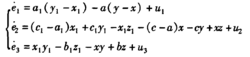
自适应控制目标是寻找合适的控制器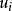 以及参数自适应律，使得系统式（6）能全局渐近同步于系统式（1），即 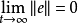3。

1963年，Lorenz发现了第一个混沌吸引子——Lorenz系统，从此揭开了混沌研究的序幕。人们不断发现新的混沌奇异性，不断地加深与统一对混沌的理解。1999年，美国休斯顿大学陈关荣教授发现了一个新的混沌吸引子——Chen系统，即陈氏混沌系统，它与Lorenz系统类似，但不拓扑等价而且更复杂。

Lorenz系统和陈氏混沌系统分别属于两个相反的类：

Lorenz系统满足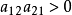 ，而陈氏混沌系统却满足 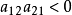，在这种意义下，他们是对偶的两个动力系统。由于陈氏混沌系统比Lorenz系统具有更复杂的拓扑结构和动力学行为，这一方面使得它在信息加密和保密通信等领域有着更广阔的应用前景，另一方面使得陈氏混沌系统很难控制，许多对Lorenz系统轻而易举的控制方法对陈氏混沌系统却不太理想甚至无效。尽管如此，目前对该系统的控制已有不少有效的控制方法，如：逆最优控制、识别控制、数字控制、模糊控制、脉冲控制、自适应控制等，随着研究的不断深入，在实际应用中必然要追求实施控制的有效性、代价大小和难易程度。