[科普中国]-交叉耦合控制

基本思想

在传统的轮廓加工数控系统中，无论是单轴控制还是多轴控制，其控制目标就是单轴的实际位置与指令位置之间的误差，即各独立运动轴的跟踪误差。轮廓误差是轮廓加工中最重要的误差，最终加工出的轮廓是由多运动轴的协调运动形成的。如果只对单一轴的误差进行控制而不顾及其它运动轴当前的误差以及运动情况，加工出的廓形就会产生较大的误差，尤其是在高速情况下，当各运动轴的参数存在差异的情况时，就会因为参数的不一致，造成加工轮廓的变形。基于这种情况考虑，一种自然的想法就是，每一个单轴的位置控制器不单单只接收来自本轴的误差及运动信息，还需要实时接收当时其它运动轴的误差及运动信息，以使本轴的运动与其它轴的运动协调起来，这就是多轴交叉耦合控制的基本思路。

普通的多轴控制系统中，由单独的每轴闭环控制产生的误差为各自理想位置和实际位置之间的距离，且单独由每轴的位置所补偿。实际上，整个控制系统的误差是由多个运动轴的位置误差共同决定的。故有人提出多轴交叉耦合控制概念。以多轴交叉耦合控制为基础，根据整个控制系统的误差对各个轴进行误差补偿，控制的目标是减少整个多轴系统的误差。1

基于每个轴的跟踪误差来直接反映轮廓误差，通过交叉耦合控制器进行运算得到每个轴的位置补偿值。然后，将每个轴的位置补偿结果加至每个轴的位置给定中，从而确保每个轴都能够反映其他轴的动态特性变化，最终消除每个轴对其他轴的影响。交叉耦合控制器可以认为是底层控制器与高层控制器的结合运用，从自动控制的角度看，通过耦合轮廓补偿的方法改善系统轮廓精度的实质是将系统开环的轮廓控制变为闭环轮廓控制。

交叉耦合控制器结构针对平面轮廓误差模型，Kroen 提出了相应的交叉耦合控制器，它提供了很好的解决方法和思路，几乎是所有轮廓误差控制算法的起源，其控制算法的思路主要是：先将从两正交轴所测得的跟踪误差进行耦合，计算出轮廓误差，然后经过一个比例控制器（CCC），分解到各个正交轴的输入端。其结构如下图所示。这个交叉耦合控制系统实现了将输入量即跟踪误差转变为反馈控制所需要的轮廓误差。2

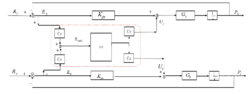
求轮廓误差的方法，实际上是对自然坐标系下得到的跟踪误差进行了坐标变换，将其变换成为加工轮廓切线方向和法线方向的误差，其中切线方向上的误差的体现了系统时滞性，而法线方向上的误差，就是轮廓误差的体现。

由 Kroen 的交叉耦合控制系统可知，补偿系统是以轮廓误差模型为基础的。所以对于更为复杂的空间轮廓误差模型，其对应的控制系统在结构上，以及内部算法都会比较复杂，增益匹配模型也会变得较为复杂。

控制方法所谓的交叉耦合控制器，通常情况下是由两部分组成，一部分是实时计算轮廓误差的轮廓误差计算模型，另一部分是将所得的控制量按照一定的关系分别补偿到各运动轴的轮廓误差分配控制器。轮廓误差分配控制器可以综合考虑到各平动轴的参数不匹配以及运动不协调等诸多藕合因素以及不稳定地干扰源，因此，在多轴控制中通常会考虑使用交叉耦合控制器及其改进模型进行误差的综合补偿。其基本思想是根据各独立轴的所反馈的信息，实时计算轮廓误差的大小并通过控制策略进行补偿信号的输出，然后按照一定的关系将输出信号分配到各运动轴上，从而达到减小轮廓误差，控制定位精度的目的。从控制学的角度来看，通过交叉藕合轮廓补偿的方法改善系统轮廓精度的实质是：将系统开环的轮廓控制转变为闭环的轮廓控制。而闭环的控制相对于开环控制的特点就是，稳态误差小，控制精度高，但是却存在系统不容易稳定的缺点。

交叉耦合控制器的两个主要模块就是用于实时计算轮廓误差的误差计算模型，以及误差补偿量的分配模型。如下图所示。

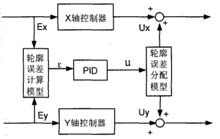
其中，轮廓误差 就是系统用于实时计算轮廓误差的误差模型，u就是用于误差补偿量的分配模型。3

参数优化方法为了实现交叉耦合控制器参数对轮廓误差具有自适应调整的能力，不得不进一步对交叉耦合控制器参数优化算法进行研究。其控制策略的思路为：在经典 PID 控制策略的基础上，添加能够使交叉耦合控制器 PID 控制参数根据轮廓误差大小进行实时自适应变化的自适应模块。这个自适应模块是通过一些先进控制方法的应用，实现交叉耦合控制器参数对轮廓误差的自适应调整。其结构框图如下图所示。对于轮廓误差补偿量的分配方式，选择比例误差分配。对于 X ，Y 两轴联动的交叉耦合控制器参数优化算法，采用经典 PID 控制与先进控制方法相结合的方式，从而得到能够在系统运行过程中，实现 PID 控制参数对轮廓误差自适应调整的参数优化方法。

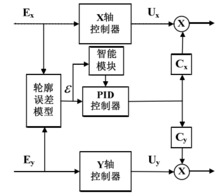
为了实现交叉耦合控制器参数能够对磨削系统任意时刻轮廓误差的自适应变化，学者们对交叉耦合控制器参数的自适应优化方法做出了大量的研究。在经典 PID 控制策略的基础上，采用众多的先进控制方法对 PID 控制器控制参数进行参数整定，如基于模糊逻辑控制的参数整定算法、基于神经网络控制的参数自适应整定算法、基于PDFF 与 H∞次优方法结合的控制算法、基于模型参考自适应的控制算法以及基于遗传算法的控制器参数整定算法等。4