[科普中国]-广义回归神经网络

简介

在机器学习和认知科学领域，人工神经网络（英文：artificial neural network，缩写ANN），简称神经网络（英文：neural network，缩写NN）或类神经网络，是一种模仿生物神经网络(动物的中枢神经系统，特别是大脑)的结构和功能的数学模型或计算模型，用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。广义回归神经网络是建立在数理统计基础上的径向基函数网络，其理论基础是非线性回归分析。GRNN具有很强的非线性映射能力和学习速度，比RBF具有更强的优势，网络最后普收敛于样本量集聚较多的优化回归，样本数据少时，预测效果很好，网络还可以处理不稳定数据。一般可以通过径向基神经元和线性神经元可以建立广义回归神经网络。

GRNN 在结构上由四层构成，分别为输入层、模式层、 求和层和输出层。输入层神经元的数目等于学习样本中输入向量的维数， 各神经元是简单的分布单元， 直接将输入变量传递给模式层。模式层神经元数目等于学习样本的数目n，各神经元对应不同的样本。求和层中使用两种类型神经元进行求和。输出层中的神经元数目等于学习样本中输出向量的维数 k， 各神经元将求和层的输出相除，经元 j 的输出对应估计结果 Y (X) 的第 j 个元素。

径向基函数网络在数学建模领域，径向基函数网络（Radial basis function network，缩写 RBF network）是一种使用径向基函数作为激活函数的人工神经网络。径向基函数网络的输出是输入的径向基函数和神经元参数的线性组合。

RBF神经网络的基本思想：用RBF作为隐单元的“基”构成隐藏层空间，隐藏层对输入矢量进行变换，将低维的模式输入数据变换到高维空间内，使得在低维空间内的线性不可分问题在高维空间内线性可分。

BF是具有单隐层的三层前向网络。第一层为输入层，由信号源节点组成。第二层为隐藏层，隐藏层节点数视所描述问题的需要而定，隐藏层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负线性函数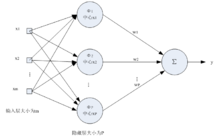，该函数是局部响应函数，具体的局部响应体现在其可见层到隐藏层的变换跟其它的网络不同。以前的前向网络变换函数都是全局响应的函数。第三层为输出层，是对输入模式做出的响应。输入层仅仅起到传输信号作用，输入层和隐含层之间之间可以看做连接权值为1的连接，输出层与隐含层所完成的任务是不同的，因而他们的学习策略也不同。输出层是对线性权进行调整，采用的是线性优化策略，因而学习速度较快；而隐含层是对激活函数（格林函数，高斯函数，一般取后者）的参数进行调整，采用的是非线性优化策略，因而学习速度较慢。

径向基函数神经网络的优点：逼近能力，分类能力和学习速度等方面都优于BP神经网络，结构简单、训练简洁、学习收敛速度快、能够逼近任意非线性函数，克服局部极小值问题。原因在于其参数初始化具有一定的方法，并非随机初始化。1

径向基函数径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。在神经网络结构中，可以作为全连接层和ReLU层的主要函数。

构造神经网络的基本方法为假设某种过程是属于某种函数空间的函数，然后连接成神经网格，运行一段时间该网络的电势趋于最小达到某种动态的平衡，从而可以求出该函数，而选择径向基函数空间是一个比较简单的容易用神经网络实现的方法。2

在乙肝发病数时间序列预测中的应用背景近年来，国内广泛展开了传染病的早期预测预警的研究，对传染病的发生、 流行及其变化趋势的预测方法主要有回归预测模型、 时间序列模型、 传染病传播动力学模型等方法。回归预测以及传播动力学模型的研究集中在对其因果关系的分析上，然而影响传染病发病的因素众多，所需的许多影响因素的数据难以收集，所建立的模型不能全面和本质地反映所要预测动态数据。基于时间序列的预测是一种较为简单的传染病预测方法，许多时间序列分析的模型等已经广泛地应用于传染病预测当中，如马尔科夫链模型、 灰色预测模型、 自回归移动平均模型等。其中，人工神经网络以其独特的并行结构、 自适应、 自组织、 较强的容错性、 鲁棒性等特点和独特的信息处理方法，在时间序列预测领域得到了广泛的应用。

目前， 在预测时用的最多的是反馈 BP 神经网络 BPNN(Error Back Propagation neural network)模型， 但该模型在训练时存在收敛速度慢和容易陷入局部极小的缺点，预测效果可能达不到预期效果广义回归神经网络GRNN(Generalized Regression Neural Network)。GRNN 收敛于样本量积聚较多的优化回归面，并且在样本数据较少时， 预测效果也较好。因此，GRNN 在多个各个领域得到了较为广泛的应用。然而它在传染病预测领域的报道仍然较少。

乙肝是一种典型的肠道传染病， 呈现周期性流行特征。乙肝传染性强， 在我国流行程度较为严重， 探讨有效的预测方法对乙肝的流行的预防控制具有重要意义。本文拟使用我国内地法定报告的 2005 年 －2011 年乙肝月发病数时间序列为建立广义神经网络模型，探讨广义回归网络在乙肝发病预测当中的实用价值。

实验条件以我国 2005 年 －2010 年这 6 年的月发病数据作为训练样本， 以 2011 年 12 个月的发病数作为验证样本， 分别建立 GRNN模型和传统的 BP 神经网络预测模型(BPNN)， 进行预测对比实验。模型的建立均在 Matlab 7.5 环境中实现。首先使用 Matlab 当中自带的归一化函数 mapminmax( )将发病数资料归一化，归一化的目的是取消数据间数量级的差别，避免因为输入输出数据数量级差别较大而造成网络预测误差较大。神经网络时间序列模型一般选取时间序列的周期长度作为模型的输入节点数。发病数资料的周期一般为一年。因此选取 12 作为本研究的输入节点数， 即使用拟合或预测样本的前12 个值作为当前训练本。另外，本研究选取常用的单步预测法， 迭代预测验证样本的发病数， 因此输出节点设为 1。光滑因子是 GRNN 中的重要参数，本研究分别设定其值为以 0.1 为步长 0.1 到 2.0 之间的值，使用 K- CV 法(本研究中取 K =3)训练模型， 循环验证， 选取最优模型， 确定最终网络结构。相对与GRNN， BPNN 模型当中设定的参数较多， 本研究仅使用 K- CV 法筛选 BPNN 的隐藏节点数， 隐藏节点分别设为 3 － 50， 循环验证， 选取最有网络结构。隐含层神经元传递函数选择正切 S 型函数，输出层选择线性传递函数， 学习函数选择 Levenberg_Mar-quardt 的BP算法训练函数， 学习速率设为 0.01， 目标精度为0. 001，网络反复训练 1000 次。

试验结果与分析经过筛选，最终确定 GRNN 模型的光滑因子值为 0.5，BPNN 的网络结构为 12 －5 －1， 两种模型的预测结果和比较如表1和图 所示，GRNN 与 BPNN 的预测值与真实值的MAPE 均控制在 10% 以内， 表明两种方法均具有较好的预测效果，其中 GRNN 所得的训练样本及预测样本的 MAE， MAPE 以及 MSE 均小于 BPNN， 因此认为， 在本次建模当中 GRNN 较BPNN 有较好的拟合效果及预测效果。BPNN 在本次建模当中预测效果相对欠佳。结果表明， GRNN 模型具有更好的拟合效果及预测效果，对于传染病的预测具有良好的实用价值。相对于 BP 模型，GRNN模型的优点是模型结构简单， 需要调整的参数少， 预测速度快，并且避免了繁琐、 冗长的数学计算， 有较好的应用前景。3