[科普中国]-分层建模

分层建模，是将多输入多输出建模问题分解为一系列单输入多输出的数据建模问题，提高多输入多输出系统建模的效率和准确性。分层建模方法克服了包括被认为是建模障碍的多元共线性在内的一类大系统中普遍存在的困难。模型中所包含的变量比其它方法所建立模型包含的变量多许多。因而模型更具有普遍性，用于预测及用于大系统的全面分析效果都好些。

对于样本集合

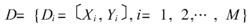
其中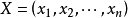 为系统的输入变量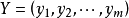， 为系统的输出变量,多输入多输出系统的数据建模问题就是确定一个向量函数F(X)，使得样本集合D满足这一映射关系F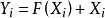， ，即

在一定的精度要求下,系统变量之间的函数关系可以近似为Y=F(X)，即

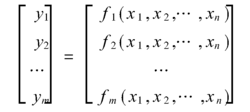
数据建模问题就是获得这种映射关系，使得在某种意义下， F是系统的最佳逼近。通常是选择一组基函数进行线性组合，给出F的一种含参变量的表达式，然后通过最小二乘法或者其它方法确定参变量的系数。数据进化建模则采用遗传编程算法自动生成映射关系的结构。同时借助于数值优化方法确定模型中的参变量，从已有解出发根据个体的适应度信息指导搜索过程向改进解的方向发展。使生成的模型个体按照一定的指标逼近样本数据。并进一步分析所获取的模型是否真实地反映所观测的系统。

对于数据建模问题，如果输入和输出变量是多维的，直接在多维模型集中搜索和生成问题的最优模型，问题的难度增大，计算的效率也显著降低。可以从两个方面将建模问题进行简化，以降低问题的复杂程度：

（1）引入问题的先验知识模型，扩充可行模型的空间域，提高问题可行解集的搜索概率；

（2）将多输入多输出建模问题分解为一系列单输入多输出，甚至是单输入单输出的数据建模问题，缩减每次建模时模型集的维数，重复地在单输入模型集中进行搜索和组合函数式，显著地降低模型搜索的空间，提高搜索效率。

从大量的工程数据或图表中可以看到，在不同的工作条件下可以获得大量的数据，曲线形状比较接近，这些数据可以用一组相同的函数模型来表示，只是模型的参数不同，构成函数模型族。

下面引入层函数的定义，对多维函数进行分解1。

层函数：对于任意一个连续的n 维输入向量函数Y= F(x1，x2，… ，xn) (n>1)，由原函数推导的一维输入变量函数称为层函数，Y=G( xk，θ)，其中θ为层函数的参数向量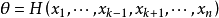， 为层函数的参向量函数，是其它输入变量的函数。

除了在某些特殊点下，函数模型可能产生退化现象外，函数的结构基本上保持不变。因此根据一组样本数据总是能够找到一个反映输入变量和输出变量之间函数关系的通式，当其它输入变量的取值改变时，只需要调整参变量的值，使这个通式能够表示所有的样本数据。

对于样本数据集D，输入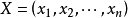变量 和输出变量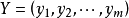 ，为了确定X 和Y之间的函数关系Y=F ( x1，x2，… xn ) ( n> 1)，先固定变量x2，x3，… ，xn为常数，组织数据集，寻找Y和x1之间的函数关系，并且用带参的结构表示。

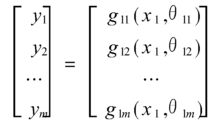
即得到第1层函数式Y= G1 (x1 ，θ1) ，其中θ1= (θ11 ，θ12 ，… ，θ1m)为1层函数的参数向量。

输入变量x 2 ，x 3 ，… ，xn 取不同的数值时，保持Y= G1 (x1 ，θ1)这个含参数的函数式，对参数向量进行优化，得到相应的参数向量θ1 的值。整理参数向量θ1 和其余的输入变量x2，x3，…，xn 的数据，重组建模的数据集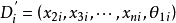， ，参数向量作为降维建模系统的输出变量，进一步获得参数向量与其它输入变量之间的函数关系。重复以上过程，直至得到原系统的最后一个输入变量与上一层函数模型中参数向量之间的函数关系式。将各层函数模型中引入的参变量逐层用下一层函数式所取代，得到多输入多输出数据的模型。其建模过程可以表示为：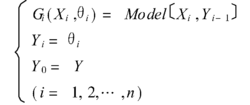

数据分层建模算法的结构描述如下：

PROCEDURE多输入多输出数据分层建模算法

{

输入建模数据集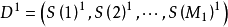

For k= 1: 1 : dimension-input-variable

{

选择本层函数的输入变量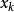

任意选取一组数据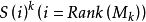

数据进化建模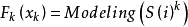

将模型转换成含参数的形式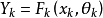

for j= 1: 1: Mk

{

参数优化θk=Opt {Fk(xk ,θk )| }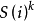

}

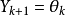
重构建模数据集

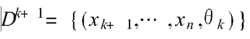
数据集分组

}

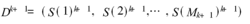
for k= (dimension-input-variable-1) : -1: 1

{
　　θk+ 1= Yk

替换模型中的参数Yk= Fk ( xk ,θk )

}

}

分层建模方法的优点是：

（1）可以直接根据数据将系统分成若干个部分，分成二个层次，而且如果条件允许，用本方法还可建立更多层次的系统模型。显然，这样的模型一般更接近于实际系统。这样的模型对于一些缺少先验知识的大系统的定性定量分析是有益的。

（2）由于分二个层次，分二次估计参数，因而分散了系统辨识的难点，可以比较容易辨识结构比较复杂的模型，不同结构的子模型（第一个层次）可以升存于同一个模型之中，这样就大大扩大了可辨识模型的范围。

（3）分层建模方法克服了包括被认为是建模障碍的多元共线性在内的一类大系统中普遍存在的困难。模型中所包含的变量比其它方法所建立模型包含的变量多许多。因而模型更具有普遍性，用于预测及用于大系统的全面分析效果都好些。

（4）分层建模可以充分利用现有的统计资料，尤其适用于数据长度一般，但截面资料丰富的情况，因为充分利用截面资料弥补了历史资料的欠缺，因而对于大系统的辨识及参数估计都有较大的影响。

（5）由于寻找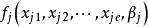 的工作，所有的建模工作都要做，而且为了寻找合适的模型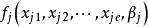， 这样的函数都要找多个，进行比较，以决定取舍，所以分层建模方法所新增加的工作，主要在第二个层次综合。个柱面方程，若采用准则C是复杂一些，计算量比较大，但若采用准则A、B ，则仍是很简单的，总之，增加的工作量不大，计算机上进行，工作增量是可以接受的2。