[科普中国]-混沌系统

混沌现象是在非线性动力系统中表现的确定性、类随机的过程，这种过程既非周期又不收敛，并且对于初始值具有敏感的依赖性。混沌理论（Chaos theory）是关于非线性系统在一定参数条件下展现分岔（bifurcation）、周期运动与非周期运动相互纠缠，以至于通向某种非周期有序运动的理论。

混沌理论在许多科学学科中得到广泛应用，包括：数学、生物学、信息技术、经济学、工程学、金融学、哲学、物理学、政治学、人口学、心理学和机器人学。

一个一维离散时间非线性动力学系统定义如下：

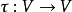其中， ， k=0,1,2,3…，我们称之为状态。 而 是一个映射，将当前状态xk映射到下一个状态xk+1。如果我们从一个初始值x0开始，反复应用 ， 就得到一个序列 ，k=0,1,2,3…..。这一序列称为该离散时间动力系统的一条轨迹。

一类非常简单却被广泛研究的动力系统是logistic映射，它起源于虫口模型。其定义有多种形式。

其中一种形式为：

其中，混沌域为(0,1)， 称为分枝参数，xk ∈(0,1)。

混沌动力系统的研究工作指出，当3.5699456…