[科普中国]-线性随机系统

随机控制系统是受随机因素影响的动态系统。线性系统是指同时满足叠加性与均匀性（又称为其次性）的系统。

线性随机系统即同时满足线性系统和随机控制系统特性的系统，它满足线性系统的叠加性与均匀性，同时又受随机因素影响。线性随机系统分为连续线性随机系统和离散线性随机系统1。

考虑如下形式的连续时间随机线性系统：

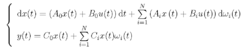
其中

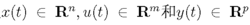
分别表示系统的状态，控制和输出向量。 为定义在全概率空间

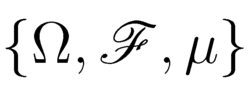
上的随机变量序列，且为独立的广义稳定的二阶矩过程。对于给定的初始条件x (0) = x0 ，我们定义其相应的解过程为x (t, x0)，输出过程为y (t, x0)。定义矩阵组A，B，C如下：

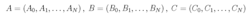
对于上述连续时间随机线性系统，当u (t)=0，t>=0时，如果有

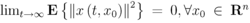
成立，就称该系统为均方稳定的，简称矩阵组A是均方稳定的。

对于上述连续时间随机线性系统，若存在矩阵K，使得当u(t) =Kx(t)时，下述闭环系统

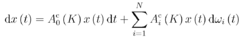
对任意的初始条件x0 2 Rn为均方稳定的，那么就称系统(2-13)为可镇定的。简称(A,B)为均方可镇定的。

其中，

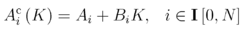
如果存在常数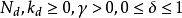使得

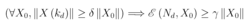
那么就称(A,C)为能检测的。

其中

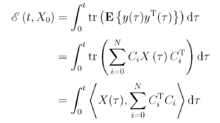
该函数可以看成是连续时间线性随机系统的输出能量函数。

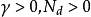如果存在常数使得

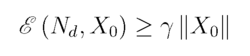
对任意初始条件x0成立，则称连续时间线性随机系统为能观测的。

我们考虑如下形式的离散时间随机线性系统：

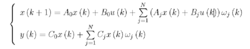
如果存在整数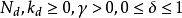> 0使得

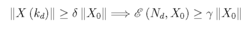
那么我们说(A,C)是能检测的。

对于离散时间随机系统，如果存在常数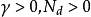使得

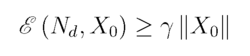成立，则称连续时间线性随机系统为能观测的。