[科普中国]-线性时变系统

基本概念

线性系统是指同时满足叠加性与均匀性（又称为其次性）的系统。所谓叠加性是指当几个输入信号共同作用于系统时，总的输出等于每个输入单独作用时产生的输出之和；均匀性是指当输入信号增大若干倍时，输出也相应增大同样的倍数。

时变系统(time-varying system)其中一或一个以上的参数值随时间而变化，从而整个特性也随时间而变化的系统。时变系统的特点是，其输出响应的波形不仅同输入波形有关，而且也同输入信号加入的时刻有关。

线性时变系统即同时满足线性系统和时变系统特征的系统，它满足系统叠加性与均匀性的特点，同时，当系统中某个参数值随时间而变化时，整个特性也随时间而变化。

线性时变系统的表示状态方程n维线性时变系统的状态方程为：

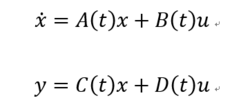
其中，u是p维输入向量，y是q维输出向量。A、B、C、D分别是线性系统的参数，均是时间t的函数，即参数随时间的变化 变化。

结构图线性时变系统的结构图如下：

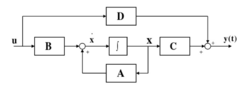
线性时变系统的能控性和能观性能控性对于线性时变系统，当t0时刻其x值为x0，在定义时间[t0,t1]时间内，状态完全能控1的充要条件是Gram矩阵

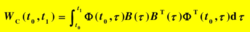
非奇异。式中Φ(t,t0)为时变系统状态转移矩阵。

推论1（秩判据）：

假设矩阵A(t)和B(t)都是n-1此连续可微的，在时间区间[t0,t1]上，若有

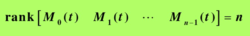
则系统状态完全能控，其中分块矩阵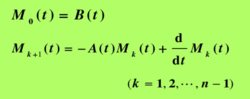

推论2（秩判据）：

假设矩阵A(t)和B(t)都是n-1此连续可微的，在时间区间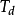 上是n-1次连续可微的，若对初始时刻 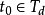，存在有限时刻 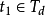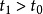， ，使得

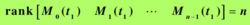
则系统在时刻t0是状态完全能控的，其中分块矩阵

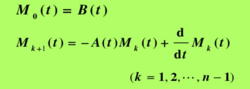
能观性线性时变系统

在定义时间[t0,t1]时间内，状态完全能观的充要条件是Gram矩阵

为非奇异。

推论1（秩判据）：

假设矩阵A(t)和C(t)都是n-1次连续可微的，在时间区间[t0,t1]上，又有

则系统是状态完全能观的，其中分块矩阵

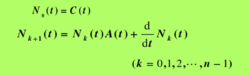
推论2（秩判据）：

对于连续时间线性时变系统，假设矩阵A(t)和C(t)都是n-1阶连续可导的函数矩阵，则系统在时刻t0状态完全能观的充要条件为：在一个有限时刻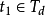 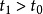， ，使得

则系统是状态完全能观的，其中分块矩阵

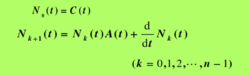
线性时变系统的稳定性稳定性是设计控制系统的最基本要求2。

线性时变系统方程：

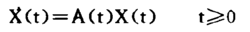
如果已经求出矩阵A(t)的所有特征值，系统渐近稳定的充要条件是：A(t)的所的特征值都位于S的左半平面。