[科普中国]-谐波状态估计

背景

随着大量非线性负荷的投入使用，越来越多的谐波注入到电网中，使得电网谐波污染引起的电能质量问题越来越严重。为有效地治理谐波，必须首先确定电网谐波的分布与状态。但在感兴趣的所有节点上都安装电能质量监测装置是不可能的，为此，需根据有限节点上测量的各次谐波电压和电流值，通过网络分析估算出未知节点的各次谐波电压以及各支路的谐波电流，以掌握整个系统的谐波状况，为谐波分析和治理提供科学的依据，这就是电力系统谐波状态估计问题。1

发展概况早期的谐波状态估计技术选取功率作为量测量是受到传统电力系统状态估计影响的结果，但因谐波无功功率的定义存在争议且其测量装置没有统一的标准，由此，采用无功功率的方法依据不足。随着基于全球定位系统（GPS）的相量测量装置（PMU）的出现以及相应的广域测量系统（WAMS）在电力系统的逐步建设，调度中心可以获得一种新型的实时测量数据———相量量测，它主要包括节点电压的幅值、相角量测和支路电流的幅值、相角量测， 有的系统还包括发电机节点的功角量测。2

与SCADA系统相比，相量量测主要有以下几个特点：增加了一种测量类型，即相角量测；数据测量精度高，这主要源于测量装置的等级高以及数据测量同步性好，即测量同步误差小两方面；数据采集、传输速度非常快。由于技术的发展，谐波量的同步测量成为可能，为此，近年来在谐波状态估计研究中基本采用谐波同步相量作为量测量，而不采用功率作为量测量，这样可使得状态估计方程线性化，计算量减小并可提高估计的精度。

目前，谐波状态估计研究主要集中在谐波状态估计建模、谐波状态估计的求解算法、谐波状态估计的可观性和误差、PMU 量测优化配置等方面。1

谐波状态估计技术国外对于谐波状态估计问题研究较早，1989年著名学者Heydt就提出了谐波状态估计问题，认为谐波状态估计是谐波潮流的逆问题，并提出了一种利用最小方差估计器的谐波源识别算法。作者利用关联矩阵建立了谐波量测量与状态变量之间的数学模型，选用注入视在功率和线路视在功率作量测量，并将节点分为非谐波源和可疑谐波源两种类型，以减少未知状态变量的数目。但是在波形畸变的情况下，无功功率的定义尚未得到统一认识，因此采用视在功率的方法欠缺说服力，但研究开创了谐波状态估计研究的先河，具有重要的意义。

Meliopoulos 和张帆等人的研究成果中将谐波状态估计问题看作为优化问题，并给出了一种最小方差估计算法。

Ma Haili和Girgis在1996年提出了一种应用卡尔曼滤波器识别谐波源的新算法，适用于非平衡三相电力系统中谐波测量仪表的优化配置，以及谐波源位置及其注入电流大小的最优动态估计。以谐波电流为状态变量，谐波电压为量测量，建立状态方程和量测方程。对于确定数目的谐波测量仪表，通过计算不同配置条件时误差协方差矩阵的迹，得到谐波测量仪表的最佳配置方案和谐波注入的最优估计值。

由于电网中非谐波源母线的数量可能远大于谐波源母线数量，为减少未知状态变量的数目，杜振平和Arrillaga提出了一种电力系统连续谐波的状态估计算法。利用关联矩阵的概念建立起谐波量测量与状态变量的数学模型，并且将系统母线分为非谐波源母线和可能的谐波源母线两种类型；此外，还将可能的谐波源母线分为测量母线和未测母线两类。采用上述方法可极大减少未知状态变量的数目，从而极大减少计算工作量，同时还可使谐波估计方程由欠定变为超定，增加了估计结果的可信度。

2000 年， S.S.Matair 和Watson 提出将奇异值分解（Singular Value Decomposition，简称SVD）算法用于电力系统谐波状态估计，该算法能够在系统非完全可观即部分可观、估计方程欠定时的情况下进行有效估计， 降低了对测量冗余的要求。当系统完全可观，估计方程正定或超定时，SVD 算法能给出一个唯一解，并以新西兰南岛220 kV电网为例，分别给出系统完全可观、部分可观时的状态估计结果，并且与实际值进行对比，对比结果表明奇异值分解法能够在系统可观、部分可观的情况下给出有效估计值。

选择节点电压作为状态量，母线注入电流、母线电压、支路电流同步量测作为量测量进行状态估计。对于有足够测量（超定）的方程且测量方程无病态时，通过节点编号优化，运用分层算法对测量矩阵进行预处理后再进行矩阵求解；对于测量方程病态、欠定时，采用SVD算法进行求解谐波状态估计问题，求得估计方程的最小二乘解。以IEEE14节点系统为例，建立系统模型，运用MATLAB编程仿真验证了算法的可靠性。而且，还在SVD 算法的基础上分析了部分可观系统的测量问题，进而对测量配置进行了优化。

2004 年，吴笃贵、徐政提出了一种基于相量测量装置PMU（Phasor Measurement Unit）的状态估计方法。选取节点电压相量作为状态变量，节点电压、支路电流和注入电流相量作为量测量，采用加权最小二乘法进行状态估计。

上述的谐波状态估计方法都有自己的特点，在某种特定的条件下可在一定程度上实现谐波状态估计，但也均存在一定的缺点，精度高、速度快与可观性好的谐波状态估计方法的研究还需进一步深化。1

谐波状态估计数学描述为进行谐波状态估计，需按照一定的估计准则，对量测值进行处理，以得到目标函数的最优状态值。虽然有很多方法均可应用于谐波状态估计领域，如最小方差估计、极大验后估计、极大似然估计和最小二乘估计以及由其衍生出来的加权最小二乘估计算法等，然而由于最小二乘法具有所需的先验统计知识少、算法简单、计算量小与收敛性好等特点，其在谐波状态估计领域得到了更广泛的应用。

在给定网络结线、支路参数和量测系统的条件下，谐波状态估计的量测方程可写为：

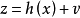
式中：

z ———量测量；

x ———状态变量，一般是节点电压幅值和相位；

v ———量测误差。

对电力系统谐波状态估计问题，引入PMU量测装置以后，存在其节点电压、支路电流和注入电流相量量测与状态量节点电压相量的线性关系，从而，谐波状态估计数学模型大大简化。在测量噪声可以忽略不计的情况下，即有如下的线性状态方程:1

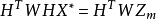
式中：

HT———量测矩阵，与系统具体的拓扑结构以及量测点的配置有关；

X*———系统状态变量；

Zm———系统量测量；

W———量测加权矩阵。

求解该方程，则得到谐波状态问题的最优估计值。

在此基础上，对于同一个系统的状态方程，应根据量测的不同情况采用不同的求解算法。3

量测点的优化配置谐波状态估计的质量是量测数量和量测装置安装地点的函数。在实际电力系统中，具有谐波量测功能的装置的配置毕竟是有限的，从经济角度考虑不可能在感兴趣的所有节点都装设。因此，在有限数量的量测装置情况下，为达到状态估计的目的，需要进行量测点最优配置问题的研究，以得到最优量测装置数量及量测点位置。

Heydt 首次提出采用系数矩阵的最小条件数法进行谐波量测点配置。针对静态谐波状态估计提出了一种混合非线性最小二乘法，然而，它研究的是选择一个最优位置放置一个量测装置来确定谐波源的问题，而不是选择量测装置的最优数量和对谐波数量的准确估计的评价。

通过算例分析比较了粒子群算法与遗传算法、枚举法在量测配置方案的计算收敛速度，对安装不同数量量测设备的配置问题，应用粒子群算法能够得到最优解，并且收敛速度相对较快。1

研究展望a）进行谐波状态估计中发电机、变压器、输电线路以及谐波源等模型建立方面的进一步研究。

b）对谐波状态估计算法进一步研究，可以借鉴现有电力系统基波状态估计方法，提出更具普遍和实用性的新算法。

c）对量测点的优化配置原则进一步研究，在保证系统可观性的条件下合理布局量测设备的安置地点，以更经济的方式使状态估计的结果质量更高。

d）研究与开发具有同步时标的电能质量监测设备，综合监控电能质量各个指标，降低PMU的投资成本。

e）开展谐波状态估计的应用研究，在应用过程中不断提高谐波状态估计的精度，使该项研究尽早实用化。1