[科普中国]-不相关变量

基本概念

不相关变量是指两个变量的相关系数为0的变量，是相互间没有线性关系的变量。变量间的关系主要有互不相容、对立、独立和互不相关。

互不相容：若两事件A与B不能同时发生，则称A与B是互不相容事件，或称互斥事件，记作A∩B= Φ。

对立：在互不相容的基础上再加一个条件，P(A)+P(B)=1。通俗的说所谓对立事件，有你没我，有我没你，咱俩之间必须有一个。

独立：设A，B是两事件，如果满足等式P(AB)=P(A)P(B)，则称事件A，B相互独立，简称A，B独立。

不相关：若随机变量 X 和 Y 的相关系数 r(X,Y)=0，称 X 与 Y 不相关，众所周知，独立变量一定不相关（自然要求方差有限），不独立变量也可以不相关，单位圆内的均匀分布即其一例。

判定方式两个变量是不是相关变量需要用相关系数r来判定，相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度1。相关系数r的计算方式如下：

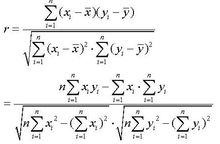
即：

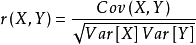其中Cov(X,Y)为X与Y的协方差，Var[X]为X的方差，Var[Y]为Y的方差。

当r=0时，称X，Y为不相关变量。

独立与不相关的关系独立和不相关从字面上看都有“两个东西没关系”的意思，但两者是有区别的。相关性描述的是两个变量是否有线性关系，独立性描述的是两个变量是否有关系。不相关表示两个变量没有线性关系，但还可以有其他关系，也就是不一定相互独立。下面是独立和不相关的关系：

（1）X与Y独立，则X与Y一定不相关。

（2）X与Y不相关，则X与Y不一定独立。

证明：

（1）由于X与Y独立，所以f(xy)=f(x)f(y)，（f为概率密度函数）

于是：E(XY)=∫∫f(xy)dxdy

=∫∫[f(x)*f(y)]dxdy

=∫f(x)dx*∫f(y)dy

=E(X)E(Y)
所以：E(XY)=E(X)E(Y)，即X，Y不相关。

（2）反例：
X=cost，Y=sint，其中t是(0,2π]上的均匀分布随机变量，易得X和Y不相关，因为：
E(XY)=E(cost sint)=（1/2π）*∫sint cost dt = 0
E(X)=（1/2π）* ∫cost dt = 0
E(Y)=（1/2π）* ∫sint dt = 0
所以E(XY)=E(X)E(Y)，但是他们是不独立的。
因为：X和Y各自的概率密度函数在（-1,1）上有值，但是XY的联合概率密度只在单位圆内有值，所以f(XY)不等于f(x)*f(y)，两者不独立。