[科普中国]-时间相关系统

如果相对于某一参考运动状态定义系统的广义坐标，就可以说系统是时间相关的。

一个简单的例子是安装在水平转台上的弹簧一质量系统，如右图（a）所示。滑块受导槽的限制，只能相对于转台沿半径方向滑动。设转台的角速度是常数，那么转角就认为是已知的，于是滑块的位置仅由径向距离来规定，这说明系统只有一个自由度。如果转台不转，那么在静平衡时，质量块的径向距离等于弹簧未伸长时的长度，即。如果转台以恒定转速转动，则系统将达到一种动态平衡状态，径向距离将是个常数（可根据牛顿第二定律确定)，且大于。假如有一个小小的扰动(例如与动平衡位置不完全一致的初始位置)施加到系统上，则会产生一个振荡性响应，其中将相对于做微小变化。至于怎样定义描述这样一种响应的广义坐标，有两种基本方法。

首先可以用一个相对于固定参考系而度量的位置坐标来描述响应，但是在此情况下发现，这样的广义坐标不够小，因为转角相当大。功率平衡法不能描述广义坐标较大的情况，因为应用功率法要求抑制(retention)非线性效应。

因此可以采用另一种办法，把质量相对于转台当前的位置作为广义坐标。例如，选作为振荡响应的广义坐标就比较合适，因为这个量对于实现线性化可以认为足够小。即便如此，由于约束力的作用，仍然不能使用功率平衡法。为什么?考虑滑块的自由体右图（b）。正压力是滑槽壁施加给滑块的约束力，它对滑块施加的运动学限制，使滑块只能相对于转台作径向运动。滑块的速度分量用极坐标表示：。因为势能考虑的是弹簧的作用，所以输入功率就是如。因，故。

这个式子从两方面说明了应用功率平衡法的困难。一方面注意到，中不含因子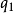，因此它与功率输入的标准公式不相符。另一方面也同样棘手，就是中出现反作用力这一事实。而使用功率平衡法处理时不变系统的初衷恰恰是为了避免考虑反作用力。约束反力出现在输入功率中，这是典型的时间相关系统。

在时间相关系统中，约束力能够造成某种特定的运动状态，而在时不变系统中，约束力的作用是防止运动发生。因此要设法导出不含(未知）约束力的运动方程。1

OSTimeDly()、OSTimeDlyHMSM()、OSTimeDlyResume()、OSTimeGet()和OSTimeSet()。

它们的功能很容易通过函数名看出来，OSTimeDly()和OSTimeDIyHMSM()都是用来延时某个任务的；OSTimeDly()只带一个参数,就是节拍数，执行它将当前任务延时给定的时钟节拍数。而OSTimeDIyHMSM()是一个格式化的延时函数，参数分别为时、分、秒和毫秒。它本质上与OSTimeDly()相同，其实就是通过调用OSTimeDly()来完成相应功能的。任务一旦被延时以后，就会处于挂起状态，每个时钟节拍到来时．内核都会检查是否延时结束，当延时结束时就将任务置于就绪态。调用OSTimeDlyResume()可以让任务提前结束延时，它是通过直接将等待时间修改为零来完成这一功能的。最后的两个函数是用来获取和设置系统时间的。2