[科普中国]-维里状态方程

定律定义

维里方程的一般表达式：

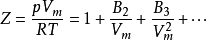
维里方程也可以用压力p的幂级数来表示

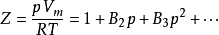
其中Vm是气体分子的摩尔体积，计算式：Vm=V/n；B2、B3分别称为第二、第三维理系数，它们与气体的种类有关，而且是温度的函数，在某一温度下，维理系数为0，实际气体行为就和理想气体近似。而且从以上两式可以看出摩尔体积越大，气压越低，则气体的行为越趋近于理想气体。当压力p→0,体积Vm→∞时，维里方程还原为理想气体状态方程。1

推导过程理想气体状态方程的表达式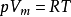： 引入压缩因子Z，其大小反映出真实气体对理想气体的偏差程度，计算定义是Z等于Vm（真实）除以Vm（理想），Z是一个趋近于1的数字，在后面加入级数来进行修正即得到维里方程。

理论上, 任何气体的状态方程, 都可以用维里形式描述:

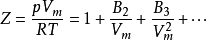
维里状态方程具有清楚的物理意义, 方程中第一项对应理想气体; 第二项描述了两个分子的相互作用; 第三项考虑了三个分子的作用, 余此类推. 对于处在高温、中高压状态下的气体, 多分子同时碰撞相互作用的情况已不可忽略,必须考虑高阶维里项. 但是, 随着维里系数阶数的提高, 计算的复杂性迅速增大, 甚至变得极其困难。2

适用范围维里方程有坚实的理论基础。用统计力学方法能导出维里系数，并赋予维里系数明确的物理意义：第二维里系数表示气体两个分子相互作用的效应，第三维里系数表示三个分子的相互作用，等等。原则上可以从理论上导出各个维里系数的计算式，但实际上高级维里系数的运算是十分困难的，目前除了简单的钢球模型外，还只能算到第三维里系数，通常维里系数由实验测定。

对于液相和汽相，维理状态方程描述一个 P-V等温过程更灵活，因为方程有较高次幂的体积、它们比三次状态方程更精确，普遍化主要是针对烃化合物。因此，对于这些化合物能够获得极好的结果，不推荐将它们用于极性化合物。

定律影响状态方程是实际气体热力计算的基础，当前常用的状态方程有B-W-R、M-H、R-K-S、P-R等方程。有的形式复杂，计算繁琐。有的由于有较强的针对性，在气体流体区内的计算精度欠佳，在热力工程应用中常受到一定限制。维里方程具有形式简明，且有明确的物理意义，但由于维里系数难于处理，在实际应用中，多限于第二维里系数以内。3维里方程在高密度区的精度不高，但由于具有理论基础，适应性广，很有发展前途。B-W-R方程、M-H方程都是在它的基础上改进得到的。