[科普中国]-概率分布标准偏差

概率分布是概率论的基本概念之一，用以表述随机变量取值的概率规律。为了使用的方便，根据随机变量所属类型的不同，概率分布取不同的表现形式。

标准差也被称为标准偏差，标准差(Standard Deviation)描述各数据偏离平均数的距离（离均差）的平均数，它是离差平方和平均后的方根，用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度，标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。平均数相同的两个数据集，标准差未必相同。

概率分布反应了该随机变量的全貌，但在实际应用中更关系代表该概率分布的若干数字特征量。这些特征量主要有期望、方差、标准偏差1。

概率分布或随机变量的标准偏差是方差的正平方根值，用符号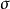 表示：

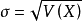
其中方差为：

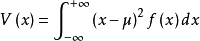
标准偏差是无穷多次测量随机误差平方的算术平均值的正平方根值的极限：

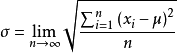
由于标准偏差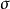 是无穷多次测量时的极限值，所以又称总体标准偏差。期望和方差（或标准偏差）是表征概率分布的两个特征参数。理想情况下，应该以期望为被测量的测量结果，以标准偏差表示测得值的分散性。

（1）二点分布

许多随机事件只有两个结果。如抽检产品的结果合格或不合格；产品或者可靠的工作，或者失效。描述这类随机事件变量只有两个取值，一般取0和1。它服从的分布称两点分布。 其概率分布为：

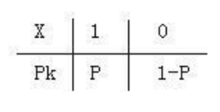
标准偏差：

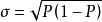
（2）均匀分布

许多随机事件只有两个结果。如抽检产品的结果合格或不合格；产品或者可靠的工作，或者失效。描述这类随机事件变量只有两个取值，一般取0和1。它服从的分布称两点分布。 其概率分布为：

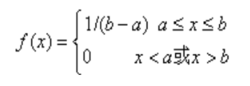
标准偏差：

假设有一批产品，不合格品率为P，从这批产品中随机地抽出n件作为被检样品，其中不合格品数X服从的分布为二项分布。X的概率分布为：

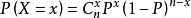
标准偏差：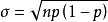

在[0，t]时间内发生冲击的次数X服从泊松分布，其分布概率为：

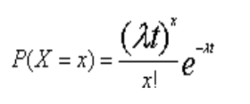
标准偏差：

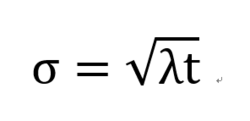
正态分布又称为常态分布或高斯分布。它的概率密度函数为：

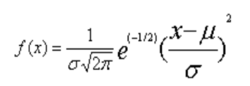
标准偏差σ的物理意义是：当一台确定的仪器对同一物理量进行n次重复测量时，表述该测量列随机误差的分散程度，σ越小。说明该仪器的精密度越好，反之精密度越差；或者，当用一台确定的仪器对一批 个（或n组）零件进行测量时，表达该组被测件随机误差的分散程度， σ越小，说明该批零件的工艺稳定性好，反之，工艺稳定性差。

标准偏差在实践中的应用主要用于2：

（1）测试仪器设备的精密度的评定；

（2）用于工艺稳定性的评定；

（3）精度检定；

（4）用于测量争议的间接仲裁。