[科普中国]-电磁波干涉

干涉条件

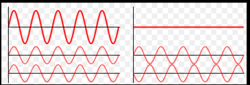两列波在同一介质中传播发生重叠时，重叠范围内介质的质点同时受到两个波的作用1。若波的振幅不大，此时重叠范围内介质质点的振动位移等于各别波动所造成位移的矢量和，这称为波的叠加原理。若两波的波峰（或波谷）同时抵达同一地点，称两波在该点同相，干涉波会产生最大的振幅，称为相长干涉（建设性干涉）；若两波之一的波峰与另一波的波谷同时抵达同一地点，称两波在该点反相，干涉波会产生最小的振幅，称为相消干涉（摧毁性干涉）。

理论上，两列无限长的单色波的叠加总是能产生干涉，但实际物理模型中产生的波列不可能是无限长的，并从波产生的微观机理来看，波的振幅和相位都存在有随机涨落，从而现实中不存在严格意义的单色波。例如太阳所发出的光波出自于光球层的电子与氢原子的相互作用，每一次作用的时间都在10秒的数量级，则对于两次发生时间间隔较远所产生的波列而言，它们无法彼此发生干涉。基于这个原因，可以认为太阳是由很多互不相干的点光源组成的扩展光源。从而，太阳光具有非常宽的频域，其振幅和相位都存在着快速的随机涨落，通常的物理仪器无法跟踪探测到变化如此之快的涨落，因此无法通过太阳光观测到光波的干涉。类似地，对于来自不同光源的两列光波，如果这两列波的振幅和相位涨落都是彼此不相关的，称这两列波不具有相干性。相反，如果两列光波来自同一点光源，则这两列波的涨落一般是彼此相关的，此时这两列波是完全相干的。

如要从单一的不相干波源产生相干的两列波，可以采用两种不同的方法：一种称为波前分割法，即对于几何尺寸足够小的波源，让它产生的波列通过并排放置的狭缝，根据惠更斯－菲涅耳原理，这些在波前上产生的子波是彼此相干的；另一种成为波幅分割法，用半透射、半反射的半镀银镜，可以将光波一分为二，制造出透射波与反射波。如此产生的反射波和透射波来自于同一波源，并具有很高的相干性，这种方法对于扩展波源同样适用。

理论基础两束光发生干涉后，干涉条纹的光强分布与两束光的光程差/相位差有关：当相位差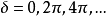 时光强最大；当相位差 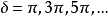时光强最小。从光强最大值和最小值的和差值可以定义干涉可见度作为干涉条纹清晰度的量度。

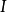光作为电磁波，它的强度定义为在单位时间内，垂直于传播方向上的单位面积内能量对时间的平均值，即玻印亭矢量对时间的平均值2：

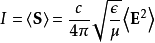
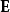从而光强可以用 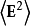这个量来表征。对于单色光波场，电矢量可以写为

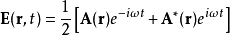
这里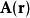 是复振幅矢量，在笛卡尔直角坐标系下可以写成分量的形式

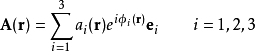
这里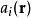 是在三个分量上的（实）振幅，对于平面波 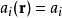，即振幅在各个方向上是常数。 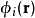是在三个分量上的相位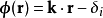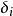， ， 是表征偏振的常数。

要计算这个平面波的光强，则先计算电场强度的平方：

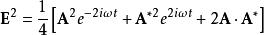
对于远大于一个周期的时间间隔内，上式中前两项的平均值都是零，因此光强为

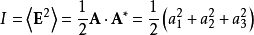
对于两列频率相同的单色平面波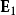 、 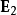，如果它们在空间中某点发生重叠，则根据叠加原理，该点的电场强度是两者的矢量和：

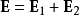
则在该点的光强为

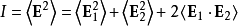
其中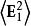 、 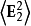是两列波各自独立的光强，而 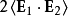是干涉项。 用 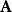、 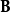表示两列波的复振幅，则干涉项中 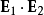可以写为

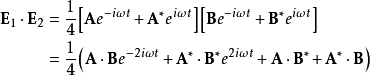
前两项对时间取平均值仍然为零，从而干涉项对光强的贡献为

根据前面复振幅的定义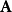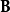， 、 可以在笛卡尔坐标系下分解为

和

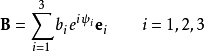
将分量形式代入上面干涉项的光强，可得

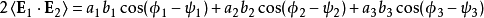
倘若在各个方向上，两者的相位差 都相同并且是定值，即

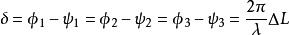
其中λ是单色光的波长， 是两列波到达空间中同一点的光程差。

此时干涉项对光强的贡献为

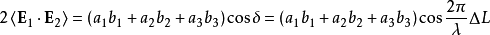
光波是电矢量垂直于传播方向的横波，这里考虑一种简单又不失一般性的情形：线偏振光，电矢量位于x轴上，传播方向为z轴方向，则两列波在其他方向上的振幅都为零：

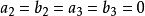
代入总光强公式：

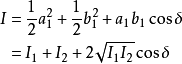
因此干涉后的光强是相位差的函数，当 时有极大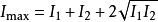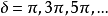值 ， 时有极小值 。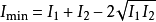

特别地，当两列波光强相同即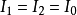 时，上面公式可化简为

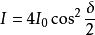
此时对应的极大值为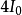 ，极小值为0。

显然，对于不同的干涉情形，产生的极大值和极小值差异是不同的。由此可以定义条纹的可见度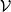 作为条纹清晰度的量度：

即可见度的范围为0到1之间。

虽然以上的讨论是基于两列波都是线偏振光的假设，但对于非偏振光也成立，这是由于自然光可以看作是两个互相垂直的线偏振光的叠加。

种类1、 相长干涉（constructive interference）：

两波重叠时，合成波的振幅大于成分波的振幅者，称为相长干涉或建设性干涉。若两波刚好同相干涉，会产生最大的振幅，称为完全相长干涉或完全建设性干涉（fully constructive interference）。

2、相消干涉（destructive interference）：

两波重叠时，合成波的振幅小于成分波的振幅者，称为相消干涉或破坏性干涉。若两波刚好反相干涉，会产生最小的振幅，称为完全相消干涉或完全破坏性干涉（fully destructive interference）。