[科普中国]-模糊性指数-

简介

模糊集是模糊数学上的一个基本概念，是数学上普通集合的扩展。用来表达模糊性概念的集合。在模糊理论中有如下定义：

1. 设Ã为一模糊集，记

Ã1={x∈A:}， 0≤α≤1

Ã0={x∈A:}， 0≤α≤1

称Ã1和Ã0分别为模糊集Ã的α-截集和α-强截集。特别地，称Ã0为Ã的支集，记作supp Ã，其中Ã0中的元素叫Ã做的支点。

2. 设Ã为一模糊集称N(Ã)为的最近寻常集其特征函数定义为

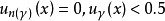
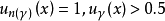
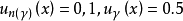
设Ã为一具有个支点的模糊集，若记

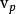（Ã）=(2/ 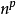).d(Ã,N(Å)

则称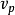 (Ã)为模糊集Ã的模糊性指数。其中d(Ã，N(Ã ))表示模糊集与其最近寻常集N(Ã )的距离。距离函数的类型并不是唯一的，这里P的值便用来反应距离函数d。通常情况下，当p=1 时距离函数d是指广义Hamming 距离，此时υ1(Ã)称为Ã的线性模糊性指数，记作υ1(Ã)。而P=0.5当时距离函数d是指Euclidean距离，此时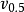（Ã）称为Ã的二次模糊性指数，记作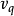（Ã）。1

模糊性与模糊集模糊性模糊性是指事物类属的不分明性。在美国数学家扎德(Zadeh，L.A.)提出模糊理论之前，系统科学的研究对象具有或不具有某种属性，明确肯定，毫不含糊，从而在数学上，元素x属于集合A或不属于集合A，非此即彼.但日常生活中，新与旧、老与少、高与矮、大与小等大量概念所反映的对象属性没有明确的界限，事物的分类常依场合或人的主观感觉不同而变化.在复杂工程问题中，误差大小、响应快慢、品质高低、决策优劣等也都难以给出精确的判别，通常只能加以定性的区分和处理。这种现象反映在数学上，必须承认不同元素可以按不同程度属于某集合或不属于某集合。总之，模糊性的数学描述是人类对事物认识和描述的一种飞跃。2

模糊性是工程实际结构中存在的另外一种不确定性。模糊性是指事物本身的概念不清楚，本质上没有确切的定义，在量上没有确定界限的一种客观属性，研究和处理模糊性的数学方法主要是模糊数学。在工程实际结构中，模糊性主要表现为：设计目标和约束条件的模糊性、载荷与环境因素的模糊性以及设计准则的模糊性。模糊性广泛存在于结构的材料特性、几何特征、载荷及边界条件等方面。

模糊集模糊数学，亦称弗晰数学或模糊性数学。1965年以后，在模糊集合、模糊逻辑的基础上发展起来的模糊拓扑、模糊测度论等数学领域的统称。是研究现实世界中许多界限不分明甚至是很模糊的问题的数学工具。在模式识别、人工智能等方面有广泛的应用。

定义

设A是集合X到[0，1]的一个映射，A：X→[0，1]，x→A(x) 则称X是A上的模糊集，A(x)称为模糊集A的隶属函数，或称A(x)为x对模糊集A的隶属度。

表示

模糊集的常用表示法有下述几种：

解析法，也即给出隶属函数的具体表达式。

Zadeh 记法，例如A=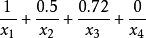 ，分母是论域中的元素，分子是该元素对应的隶属度。有时候，若隶属度为0，该项可以忽略不写。

序偶法，例如 A=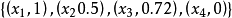 ，序偶对的前者是论域中的元素，后者是该元素对应的隶属度。

向量法，在有限论域的场合，给论域中元素规定一个表达的顺序，那么可以将上述序偶法简写为隶属度的向量式，如 A = (1,0.5,0.72,0) 。

模糊度

一个模糊集 A 的模糊度衡量、反映了 A 的模糊程度，一个直观的定义是这样的：

设映射 D : F(U) → [0,1] 满足下述5条性质：

清晰性：D(A) = 0 当且仅当 A ∈ P(U)。（经典集的模糊度恒为0。）

模糊性：D(A) = 1 当且仅当 ∀ u ∈ U 有 A(u) = 0.5。（隶属度都为0.5的模糊集最模糊。）

单调性：∀ u ∈ U，若 A(u) ≤ B(u) ≤ 0.5，或者 A(u) ≥ B(u) ≥ 0.5，则 D(A) ≤ D(B)。

对称性：∀ A ∈ F(U)，有 D(Ac) = D(A)。（补集的模糊度相等。）

可加性：D(A∪B) + D(A∩B)=D(A) + D(B)。

则称 D 是定义在 F(U) 上的模糊度函数，而 D(A) 为模糊集 A 的模糊度。

应用客观事物之间的界限具有模糊性，是模糊聚类分析产生并被广泛使用的主要原因。模糊聚类是一种无监督的学习过程，多数聚类算法需要输入参数且这些参数对聚类结果的影响比较大。得到聚类结果后, 则需要分析聚类的结果是否合理, 这属于聚类有效性研究的课题。广义上讲, 聚类有效性评价包括聚类质量的度量、聚类算法适合某种特殊数据集的程度以及某种划分的最佳聚类数目。现有的模糊聚类有效性函数大致可以分为基于数据集模糊划分和

基于数据集几何结构两类。基于数据集模糊划分的方法简单, 运算量小, 但是与数据集的结构特征缺乏直接的联系。基于数据集几何结构的方法与数据结构密切相关，但是表述复杂，运算量大。对模糊聚类来说, 有效性问题又往往可以转化为最佳类别数c的决策问题。3