公式介绍
绝热过程是在不与外界作热量交换的条件下,系统的状态变化过程。它的特征是dQ= 0。要实现绝热平衡过程,系统的外壁必须是完全绝热的,过程也应该进行得无限缓慢。但在自然界中,完全绝热的器壁是找不到的,理想的绝热过程并不存在,实际的绝热过程都是近似的。绝热的平衡过程进行中功和能的转换可根据热力学第一定律(dQ= dE+ pdV)和绝热过程的特征方程(dQ= 0)得到。即dE+ pdV= 0,从式中看出,在绝热过程中只有系统内能变化时才能作功。1
若有m千克,M摩尔的理想气体,当温度升高dT时,内能增量为 dE=(m/M)CvdT
于是 dA= pdV= - dE= -(m/M)CVdT
因为(m/M)CV是衡量,当气体由初态T1变为末态T2绝热过程中,气体作功的绝热方程为
A= -(m/M)CV(T2- T1)
由式中看出,当气体绝热膨胀而对外作功时,气体的内能就要减少,温度必降低,而压力也跟着减少。因此在绝热过程中,气体的P、T、V三个参量均同时改变。
根据热力学第一定律及绝热过程的特征(dQ= 0),可以证明,在绝热的平衡过程中,对于P、V、T三个参量之间,每两个参量间的互相关系式为
PVγ=恒量 Vγ- 1T=恒量 Pγ- 1T-γ=恒量
这三个方程称为绝热过程方程,式中γ= CP/CV为比热容比。1
绝热过程热力学系统同外界无热交换的过程。在良好的绝热材料隔绝的系统中进行的过程,或由于过程进行得很快,以致同外界没有显著热量交换的过程都可近似地看作绝热过程。例如声波在空气中的传播,以及内燃机中气体的压缩过程等,都进行得很快,可当作绝热过程处理。 在绝热的准静态过程中,热力学系统状态参量之间存在着一定的关系,称为绝热过程方程。理想气体的准静态绝热过程方程有以下三种形式:
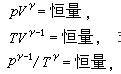
式中γ=Cp/CV,为气体定压热容同定容热容之比,且γ>1;p、V、T 分别为气体的压强、体积和温度。在p-V 图上,经过同一点的绝热线和等温线二者斜率间的关系(见多方过程)为
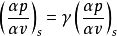
可见在p-V 图上的任意点处,绝热线都比等温线陡。 由热力学第一定律可知,在绝热过程(Q=0)中,能量转换的特点是:系统内能的减少等于系统对外界所作的功,即-ΔU=A。理想气体在准静态绝热过程中功的表达式为
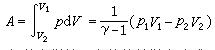
或
式中v为气体的摩尔数。 根据热力学第二定律的数学表达式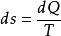 ,可见系统的熵在可逆过程中的增量 dS 等于系统所吸收的热量Q同热源的热力学温度T 之比。对于可逆的绝热过程而言,
,可见系统的熵在可逆过程中的增量 dS 等于系统所吸收的热量Q同热源的热力学温度T 之比。对于可逆的绝热过程而言,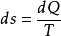 =0,即熵不变,所以可逆绝热过程即等熵过程。2
=0,即熵不变,所以可逆绝热过程即等熵过程。2
等温过程系统的温度始终保持不变的过程。等温过程的特点是温度T=恒量。对理想气体而言,在等温的准静态过程中,由理想气体状态方程得出,系统的压强和体积的乘积保持不变,即pV=恒量。理想气体经等温过程由状态I(p1,V1)到状态 Ⅱ(p2,V2)时系统所做的功
v为气体的摩尔数,T为气体的热力学温度(见热力学温标),R为摩尔气体常数。理想气体的内能仅仅是温度的函数,所以等温过程中内能的变化为零。由热力学第一定律得出,理想气体在等温过程中能量转换的特点是Q=A,即系统吸收的热量等于系统对外界所做的功。 等温过程是热力学中一种重要过程。卡诺循环就是由两个等温过程和两个绝热过程组成的。物质三态的可逆转变也是在等温条件下进行的。2
绝热过程方程导出模拟多方过程中最具有实际意义的过程主要为等容、等压、等温及绝热这四种过程.这四种过程的过程方程的建立,其难易程度相差甚远.对等容、等压、等温的过程方程可直接表述为:
V=常数 P=常数 T=常数

以上三种过程方程的建立很直观又极其容易,所以学生对它们没有丝毫的疑虑.然而绝热过程方程的建立就大不一样了.现行的热学教材上有二种不同的处理方法,一种是不作任何推导,直接地给出绝热过程方程的具体形式:
PVV=常数
另一种方式是依据绝热过程的定义,如果系统在整个过程中始终不和外界交换热量,则这种过程即为绝热过程,得出Q=0,再使用热力学第一定律和理想气体的状态方程,通过高等数学的运算,最终导出了绝热过程方程的形式.这一推导过程属于典型的“定义+定律+数学运算”的模式,缺少物理模型的参与,所以不能给学生留下直观的认知,学生对方程只知其然,不知其所以然,在学生运用该公式解答习题时会产生各种各样的疑虑,导致各种各样错误的产生.为了克服这一弊端,本文采用往返于两壁间的可视质点的弹性小球与可动壁的碰撞来模拟说明当气体被压缩时其温度升高的机理,并且能在一维方向上推导出单原子气体的结果,继而推广到三维和多原子气体分子,最终模拟导出理想气体绝热过程方程,具体模拟推导过程如下所述;如图1所示,在一个带有活塞的柱形气缸内有一单原子分子沿着气缸的长度方向,从活塞近旁以v0的初始速率朝气缸底面运动,同时活塞以u《 v0的速率向前推进.气缸的初始长度为L0,横截面积为S0,假设气缸置于无重力场的太空中,因此不用考虑重力的影响.
如图2所示,分子经Δt1时间与活塞第一次相碰,此时活塞推进的距离为ΔL1,则有
Lo+(Lo-△L1)=Vo△t1
△L1=u△t1
得△t1=2Lo/vo+u △L1=2Lou/vo+u
以活塞为参照系,分子与活塞相碰前的接近速度为v0+ u,因弹性碰撞,碰后分离速度大小也为v0+ u,故碰后相对固定的气缸,分子速率为
v1=v0+ 2uv1
为分子与活塞第一次碰撞后的分离速度,第一次相碰后,瞬间气缸长度为L1,则有
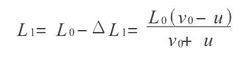
分子又经Δt2时间与活塞第二次相碰.此时,活塞又推进ΔL2间距,同理可得
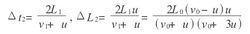
由同样的分析可知,第二次碰撞后分子运动速率为
v2=v1+ 2u=v0+ 4u
第二次相碰后瞬间气缸长度为L2,则有
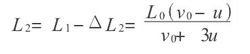
运用数学归纳法可推知,第K-1次与第K次相碰之时间间隔为Δtk,活塞在此时间间隔内推进的间距ΔLk,第K次相碰后瞬间分子运动速度vk,此时瞬间气缸长度Lk分别为
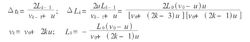
从以上几式即得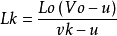
因v0>>u, vk>>u,故有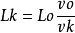
将vk近似视为连续变化,Lk也随之连续变化,用变量v,L替代,则有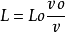
由上式可得
其中m为分子质量.又因为V0=SL0, V=SL,所以可得
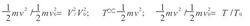
其中T和T0分别对应动能1/2mv2和1/2mv02的两个“温度”.
于是有TV2= T0V02=常数
上式为一维情况下的结果,假如设想有一个正方形容器的三个面固定,另三个面同时均称地向三个固定面推进,那么上述过程应改写为
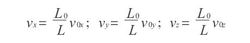
由以上三式可得
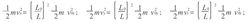
由以上三式相加可得
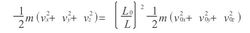
此时体积应表示为Vo=Lo3,V=L3,所以上式即为TV2/3=ToVo2/3
绝热过程方程“ PVV=常数”中的指数V为Cp/Cv,CP又等于CV+ R,作为单原子气体分子的CV为3/2R,所以当气体为单原子分子时有

即单原子分子气体的绝热过程方程应为 PV5/3=常数, PV5/3=PoVo5/3
将理想气体的状态方程 PV/T=常数,即PV/T=PoVo/To
代入上式即可得 TV2/3= ToVo2/3=常数
所以上述模拟推导最终能得到 PVV=常数3




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国