[科普中国]-圆锥补偿算法

捷联惯性导航系统SINS（Strapdown InertiaI Navigation System）在较恶劣的高动态环境下工作时，存在着较大的圆锥误差，需要对其进行补偿，否则，将直接影响精度。这种补偿算法即圆锥补偿算法。

高速、高精度的圆锥补偿算法是提高捷联惯性导航系统(SINS)性能的重要环节。圆锥误差的补偿主要与陀螺的采样周期和旋转矢量修正算法有关。缩短采样周期可以减小圆锥误差，但计算量也相应地增大。因此研究合适的旋转矢量修正算法是克服圆锥误差的有效途径。

圆锥运动是分析圆锥补偿算法的典型运动。旋转矢量微分方程的简化式：

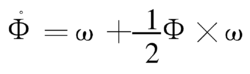
式中，Φ为旋转矢量；ω为陀螺输出的角速率。由上式可以推导出多种求取旋转矢量的算法， 如单子样、二子样、三子样、四子样和二子样迭代算法等都是工程中常用的算法，从算法精度和计算量综合比较， 三子样算法比较优越。三子样算法表达式：

Φ= Δθ1 +Δθ2 +Δθ3 +0 .45(Δθ1 ×Δθ3)+0 .65Δθ2 ×(Δθ3 -Δθ1)

式中，Δθ1，Δθ2，Δθ3 为T ～ T +h 姿态更新周期内陀螺等间隔角增量输出。而根据这3个角增量只能假定在姿态更新周期内ω为二次多项式：

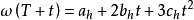式中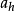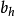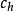， , , 为姿态更新周期h 内的陀螺角速率多项式系数。此算法的圆锥运动误差：

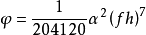式中，α为圆锥角；f为圆锥运动的角频率。

如果陀螺输出为ω时，需要用数值积分法(如梯形法或辛普生法)由ω提取角增量，再计算Φ。此时该算法的圆锥运动误差：

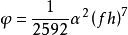
显然ω输入情况下三子样算法误差增大，原因是角增量提取过程引入误差。另外，在姿态更新周期内提取等间隔角增量时也增加了计算量1。

圆锥补偿算法的一般形式为：

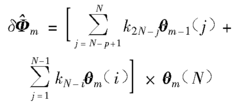
式中p 为利用的上一周期的数据采样个数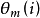； 为第m 次圆锥补偿周期的第i 个角度输出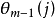；为第m- 1次圆锥补偿周期中的第j个角度输出。此表达式仍存在一定程度的误差, 需进一步修正。

当以旋转矢量描述载体姿态运动时，ΔΦ的值为：

误差判据定义为精确的更新旋转矢量ΔΦ与估计的更新旋转矢量ΔΦ'之间的差值。而它们的各分量之间只有第1项是非0常值，其余两项都呈周期性。因此，定义算法误差如下:

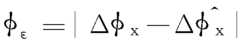
而该算法误差会在被修正的四元数中产生漂移误差，定义为

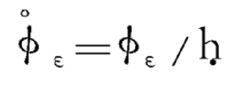
因此，圆锥补偿算法的优化准则就是让Φε的低幂次项为0，以使Φε·最小。

捷联惯性导航系统SINS（Strapdown InertiaI Navigation System）在较恶劣的高动态环境下工作时，存在着较大的圆锥误差，需要对其进行补偿，否则，将直接影响精度。国内外学者对高精度、高速度的圆锥补偿算法进行了大量的研究，取得了许多成就2。通过在典型圆锥运动条件下对算法进行优化，得到相应的圆锥补偿系数方程和算法误差表达式。这对于角速率圆锥补偿算法快捷有效的应用于工程实践具有理论意义和实用价值。