[科普中国]-电子动量谱学

简介

电子动量谱学的基本过程是电子碰撞电离（e，2e）反应，它是受核物理中的（p，2p）反应启发而发展起来的，即电子与靶粒子（原子、分子、原子团簇、分子团簇、固体薄膜和固体表面等）碰撞发生的电离过程，可以表示为：

式中Ej和Pj分别为电子的动能和动量，j=0，1，2分别表示入射电子，散射电子和敲出电子，A(i)和A+(f)表示初态靶粒子和末态剩余离子。在碰撞电离过程中，具有一定能量（keV量级）的电子束与靶物质碰撞，并使其电离，出射两个电子。利用实验核物理学中的快慢符合和多参数数据获取等测量技术，同时测量两个出射电子的能量和方位角，判定两个出射电子是否来自同一个（e，2e）事件，进而得到靶粒子轨道电子的能谱和动量谱。因此，电子动量谱学能够获得轨道电子能量-动量分布的二维信息，其中一维是电子的能谱信息，它与原子和分子的电子能级或晶体的电子能带结构相关；另一维是电子的动量谱信息，也就是动量表象中电子波函数的模平方 （通过傅立叶变换，动量表象中的波函数可以变换为坐标表象中波函数 ，这一维的信息与电子轨道的形状相关。简单地说，电子动量谱学研究的是具有一定能量的电子在动量空间中所在轨道的形状。轨道能量和轨道形状对了解原子分子的物理和化学性质，以及化学反应过程起着非常重要的作用，有助于了解化学键（成键和反键）的本性。

在电子动量谱学兴起之前，人们只能比较好地测定轨道能量，而不能精确地获得轨道的形状，因而人们虽然已经意识到轨道形状信息的重要性，但还是不能充分地获取和利用这些信息。过去人们发展了若干实验技术，试图通过测量原子分子中电子的动量分布得到波函数的详细信息。其中伽马光子的康普顿散射轮廓、高能电子散射和正电子湮灭技术不能给出束缚能信息，虽然也给出了电子动量分布信息，但是给出的是对所有轨道积分动量分布，至少是对全部价电子轨道的总和。光电子谱仪虽然能获得精确的电离能谱信息，由于光子动量很小，动量转移实际上为零，因而不能得到电子的动量分布信息，但是（e，2e）电子动量谱学能够同时提供电子轨道能量和在小动量区域（距离原子核较远的坐标空间区域）内电子运动规律。结合电子动量谱学和其他相关的实验技术以及理论方法有助于我们更准确、更全面地理解物质的电子运动规律和电子结构。

经过近四十年的发展，电子动量谱学作为研究原子、分子和固体薄膜等物质的电子态结构和电离机制的一种强有力工具，已经成为物理、化学、生物、材料和医药等多学科交叉的一个前沿领域，对电子关联效应、相对论效应、扭曲波效应、化学位移等基本的物理化学问题展开了研究，并且取得了一定的进展。随着电子动量谱学实验技术和理论方法的不断发展，电子动量谱学的研究内容和应用范围会在深度和广度上得到不断的扩展，进而推动电子动量谱学及相关学科领域的更大进展1。

基本原理电子动量谱学的目标是从实验上直接地得到靶粒子中各电子态的能量和波函数信息，它依据的基本原理可归纳为三条2:

1、利用(e，2e)反应。实验上对(e，2e)反应进行完全测量，例如在Weigold几何条件下，测定三重微分截面。

2、(e，2e)反应过程的能量守恒条件给出

其中E0，E1，和E2分别为入射电子，散射电子和敲出电子的能量，是实验上能测定的量， 是敲出电子原来在靶粒子中的结合能，这正是人们希望获取的信息。类似于光电效应中的爱因斯坦方程，因此，电子动量谱学获取电子能谱的原理与光电子谱学类似。

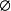3、实验上创造准自由条件。敲出电子在未被打出之前，在靶粒子中处于某一状态，它的动量不是单一的，而是具有确定的分布，由 来描述，其中p是该电子的动量， 中(p)是动量表象中该电子的波函数。例如氢原子，P主要出现在0-1.2au之间，，au表示原子单位制。怎样测定p呢?初看起来，这是一件很难做到的事。实际不然，准自由条件使p成为实验上可测定的量。理由如下:

(e，2e)反应前，靶粒子可看成在实验室系中是静止的，因此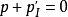 ，其中p和p'分别是反应前敲出电子和离子实的动量。反应过程的动量守恒给出:

其中p0，p1和p2分别为入射电子，散射电子和敲出电子的动量，都是实验上可测定的量，pi是反应后离子实A+的动量。一般说来pi!=pi'，但在准自由条件下，可以认为敲出电子是突然被打出来的，以致离子实A+来不及响应，只起旁观者作用。因此pi和pi'几乎相同，变成:

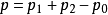
对比可知，p和pi大小相等，方向相反，虽然它们的含义是不同的。正因为这样，以后当我们只涉及动量大小时，我们也用P代表离子实A+的反冲动量。

准自由观念不但使束缚态电子动量成为可测定的量，而且使（e,2e）实验条件的实质更为清楚，例如，Wiegold几何条件下改变甲的实质就是对束缚态电子的动量大小进行挑选。

准自由观念也使（e,2e）反应的三重微分截面与动量分布函数联系起来。以H原子为例，在准自由条件下，显然有:

上式左边是实验测定量，右边的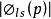 是H原子ls电子在动量表象中的波函数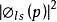， 是电子动量为p的几率， 是动量分别为p。和p的两个电子发生散射变成动量分别为p，和pZ的微分截面，即所谓Mott截面，理论上可以精确地计算出来，Const是比例常数，只与实验的几何条件有关。

常直观地表明：只要在准自由条件下实验上测定(只需相对测量)三重微分截面，就可以相当直接地得到电子的动量分布。

发展历程电子动量谱学的提出可以追溯到上个世纪五十年代初，Chamberlain和Segré利用质子束轰击锂核的（p，2p）反应，通过测量实验两个出射质子的角关联分布来研究靶质子的动量分布。1965年，McCathy在研究（p，2p）反应时发现，在波恩近似的条件下可以把（p，2p）反应的矩阵元分解为两个因子：一个是反应势的傅立叶变换形式，另外一个是原来束缚质子的波函数的傅立叶变换形式。因此，从原理上可以通过（p，2p）反应测量得到靶核中束缚质子的动量密度分布。在这样的背景下，一些核物理学家（Amaldi、McCarthy等）指出，类似的反应也可以扩展到原子分子和固体薄膜等领域，从而揭开了（e，2e）反应对原子、分子和固体薄膜的电子结构进行研究的序幕。Glassgold等人于1968年指出利用（e，2e）反应探测原子分子和薄膜中的单个电子轨道动量分布，并且讨论了电子关联效应的问题。很快，国际上相继有多个实验测量来验证这种可能。1969年Amaldi等人用非常高的能量对碳薄膜靶进行了符合测量。在同一年，Ehrhardt等人在低入射能条件下对氦原子进行了符合测量。1972年，Camilloni等人首次测量了固态碳的1s轨道动量分布，可以区分芯轨道和价轨道的差别。1973年，Weigold等人在入射能为400eV的条件下，以较好的能量和动量分辨率对Ar原子的价壳层轨道进行了（e，2e）实验测量，可以区分3p和3s亚壳层，实验中他们还观察到了多个离子末态，从而证实了电子关联效应的存在。在理论方面，Smirnov和Neudatchin于1966年从理论上指出（e，2e）反应的潜在价值。1968年，Glassgold和Ialongo导出了（e，2e）反应的平面波理论形式。Neudatchin等人又在同年给出了原子、分子和薄膜的平面波冲量近似理论形式。Levin在1972年指出（e，2e）反应可以用来研究电子关联效应。这样，随着电子动量谱学实验技术和理论方法的提出和形成，EMS作为一个新的分支学科诞生了。

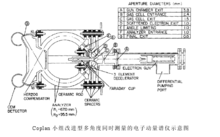
电子动量谱仪的发展回顾电子动量谱仪的发展历史，动量谱仪已经从第一代、第二代发展到现在的第三代。第一代电子动量谱仪（20世纪70年代）的特征是单能量和单角度的逐点测量，既不能对能量进行扫描，也不能对角度扫描，因而探测效率非常低。此阶段两个比较典型的谱仪有澳大利亚Flinders大学Weigold小组的谱仪（1973）和加拿大UBC大学Brion小组的谱仪（1976）。图是Brion小组的谱仪示意图。此阶段谱仪的结构都基本相似，谱仪的分析器系统由减速透镜和筒镜分析器构成，减速透镜的目的是选定两个出射电子的θ、φ角，将电子的能量减速到筒镜分析器所要求的能量，并聚焦至能量分析器的入口位置。谱仪采用通道电子倍增器探测电子，缺点是接收面积非常小，只能接收某个点上的电子。因此在某一时刻，第一代谱仪实际上只能得到单个能量和单个角度φ的符合计数，绝大部分（e，2e）事件都无法记录，效率极低，完成一个EMS实验测量大约需要半年左右的时间。第一代电子动量谱仪较低的分辨率和探测效率决定了谱仪只能进行简单原子和分子的电子动量谱学研究，例如H、He、Ar和H2等。尽管仪器的能量分辨率差和实验周期过长，很多实验结果和结论都有待于进一步确认和检验，但是第一代动量谱仪的研究成果显示出电子动量谱学所具有的潜在价值。

随着电子位置灵敏探测技术和电子分析器的发展，电子动量谱仪由第一代迈进了能量多道型或角度多道型的第二代（20世纪80年代），探测效率和分辨率都得到了明显提高，实验周期也缩短到一个月左右。美国Maryland大学的Coplan小组在1978年首次实现了多个角度的同时测量。图表示Coplan小组改进型多角度同时测量的电子动量谱仪示意图，它在球分析器的出口放置了10个电子倍增器（CEM），显然这样做的缺点是对每个CEM的一致性和稳定性要求都很高，相似的结构也被日本Tohoku大学的Udagawa小组采用。为了克服上述缺点，加拿大的Brion小组设计了一种采用二维位置灵敏探测器的多角度同时测量的电子动量谱仪，不过能量分辨率较差，为4.3eV。1984年Weigold研究小组首次研制成功了采用半球分析器和一维位置灵敏探测器的多能量同时测量的电子动量谱仪。此后，Brion小组、中国的清华大学研究小组和中国科学技术大学研究小组也各自研制成功了基于一维位置灵敏探测器和半球能量分析器可以实现多能量同时测量的第二代电子动量谱仪，这些谱仪的能量分辨大约都在1.4eV左右。澳大利亚的Flinder大学在其第二代谱仪上安装了电子能量单能器，使得其能量分辨率达到了0.55eV，目前该小组还在利用该谱仪开展工作。图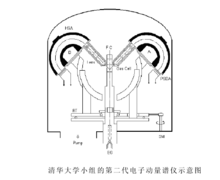是清华大学小组的第二代EMS谱仪示意图，通过旋转其中一个臂来实现对方位角的扫描。

探测效率和能量分辨率都有明显改善的第二代谱仪取得了一系列有特色的科研成果，令人们相信电子动量谱学具有巨大的应用价值。1987年，水分子1b1轨道的（e，2e）实验数据促进了量子化学理论关于电子关联效应计算的发展和完善；1990年，郑延友等人用圆偏振激光将Na原子激发，首次测量了原子激发态的电子动量谱；1995年，郑延友等人首次测量了甘氨酸（Glycine）的电子动量谱，发表在Science杂志上。虽然在第二代谱仪上取得很多重要成果，但是受到统计不确定性大和分辨率不够高的限制，而正是这些局限性阻碍了电子动量谱学将其自身潜在价值充分展示在人们面前。

电子动量谱学理论方法的发展电子动量谱学理论方法是与动量谱学实验技术相辅相承发展起来的。（e，2e）反应有多个粒子参加，在量子物理中，这是一个多体问题，当入射电子的能量比较大时，多电子原子分子的（e，2e）反应可以近似为是入射电子、靶的出射电子、靶离子的库仑三体问题来处理。对于这样的多体体系，理论上不能精确求解库仑三体问题，在实际的计算中需要采用一些近似方法。早期的电子动量理论描述采用的是平面波冲量或波恩近似（Plane Wave Impulse or Born Approximation，PWIAorPWBA）、以及靶的独立粒子理论模型近似（Target Hartree-Fock Approximation，THFA），即用HF轨道近似Dyson轨道。虽然THFA和Koopmans定理可以解释光电子谱的主要电离谱线及其电子动量谱线，但是由于THFA没有考虑到靶物质初态和离子末态的电子相关效应，THFA不能很精确地描述分子轨道电离能的实验数据（理论预测普遍比实验测量值偏高1-2eV），也不能解释由离子多组态相互作用产生的一些附加的电子相关谱线，即实验电离能谱上的伴线结构。伴随着第二代谱仪的诞生，关于电子相关效应的理论计算也逐渐发展起来，可以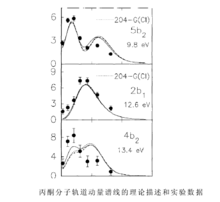说是第二代电子动量谱仪的实验成果促进了电子动量谱学理论的完善。例如，以前的理论预测是无法正确重现1987年实验测量得到水分子1b1轨道（e，2e）电离强度的实验结果的。后来量子化学计算工作者认真考虑了电子关联效应，重新做了MRCI计算，理论结果才与实验数据相符合。但是因为CI计算的复杂性，直到目前仅限于对原子和简单分子的动量谱学研究。另外，丙酮分子轨道动量谱的CI理论预测和实验测量结果之间仍存在差异，除了动力学的原因以外，还有可能是由于截断后的CI计算对电子关联作用的描述不够完全。