[科普中国]-总体标准偏差

总体标准偏差是无穷多次测量情况下的实验标准偏差，又称为理论标准差。计算公式为：

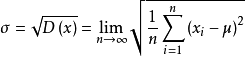只有当n充分大（例如取n为200以上）的情况下，σ才与s接近，但决不能相等。一般课本或专业书籍上， 往往把σ称为标准偏差。通常，σ是未知的，S只能作为σ的估算值。而且， 由于n的次数有限，s本身也有个不确定度。

标准偏差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准偏差，代表大部分的数值和其平均值之间差异较大；一个较小的标准偏差，代表这些数值较接近平均值。

总体标准偏差σ值小，表明测量值比较集中，σ值大表明测量值比较分散。其中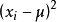， 的目的是为避免正误差和负误差相互抵消，因而取其绝对值，开方的目的是为了不改变其量纲。

可用标准偏差表征测量值的分散程度， 例如用标准偏差表征测量仪器的重复性和复现性。σ是无限次测量的误差的正均方根值，但它不是一个具体的误差。式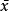 -μ=δ，实际上真值是不可知的，一般以算术平均值来作为真值μ的最佳估计值。因此，可以用 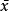代替μ，而用s作为总体标准偏差σ的估计值，此时有：

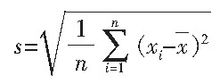
现在的问题是，S是否就是σ的无偏估计值。为了解决这个问题只要计算一下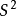 的数学期望是否是 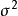。如果计算得到 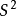的数学期望是 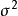，那么就说明S就是σ的无偏估计值，否则就不是。为了计算方便，先把 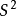写成下面的形式：

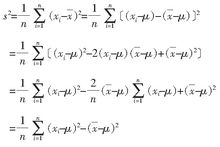
则有：

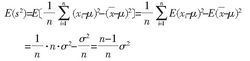
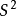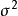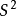由此可见， 的数学期望并不等于 ，因此 不是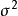 的无偏估计值。如果用 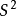来估计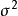 ，必然在结果中含有一个系统误差 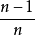。为了得到参数 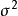的无偏估计值，只要把 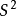乘以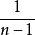 就可以了，这就是说：

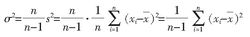
其中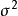， 称为总体方差。为了区别总体标准偏差，用S作为总体标准偏差σ的无偏估计值，则有：

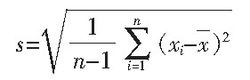
这就是著名的贝塞尔公式。对同一被测量作n次测量，表征测量结果分散性的量s，可用贝塞尔公式算出。称s为单次测量的标准偏差，一般称其为实验标准偏差，是表征测量结果分散性的重要参数。式中x为n次测量的算术平均值，xi-x=νi是残差，n-1为自由度。可以看出，计算实验标准偏差的3个重要参数是算术平均值、残差和自由度。而σ为总体标准偏差，s为实验标准偏差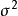， 为总体方差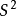， 为实验方差。

当n→∞时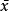， =μ，说明实验标准偏差s与总体标准偏差σ的原始定义是一致的。而在n有限时，实验标准偏差s计算所得的值只是总体标准偏差σ的一个估计值1。

总体标准偏差σ的物理意义是：当一台确定的仪器对同一物理量进行n次重复测量时，表述该测量列随机误差的分散程度，σ越小。说明该仪器的精密度越好，反之精密度越差；或者，当用一台确定的仪器对一批 个（或n组）零件进行测量时，表达该组被测件随机误差的分散程度， σ越小，说明该批零件的工艺稳定性好，反之，工
　　艺稳定性差。

可以看出，通过测量误差引出了算术平均值，通过算术平均值引出了残差和自由度， 进而引出了实验标准偏差，实验标准偏差用来表征对同一被测量作n次测量结果的分散性。而表征合理地赋予被测量之值的分散性，并与测量结果相联系的参数就是测量不确定度。因此，实验标准偏差是测量不确定度评定的重要参数，也是测量不确定度评定的理论基础。

无论是总体标准偏差σ还是实验标准偏差s，都不是一个具体的误差。它的数值大小只不过说明在一定条件下进行一系列测量时， 随机误差出现的概率密度分布情况。σ值小表明测量值比较集中，σ值大表明测量值比较分散。所以，在测量中，取测量列的算术平均值作为测量结果，用实验标准偏差表征测量值的分散程度。因此，算术平均值和实验标准偏差是测量不确定度评定的数字特征。

在编制仪器的检定规程时，除通过一定的分析计算，最终还须进行一系列的实验测试。用n次测试结果计算出 σ值，然后根据需要给定其极限误差。如我厂自制一台称重量用的测力装置。被测参数为2000kg士15% 。该装置的允许极限误差究竟给多大才合理，保证使用要求？我们用三等测力计对其进行20次等精度测量。算出 σ=4.54，我们取极限误差为3σ=15kg，证明该装置能满足使用要求。

当仪器不变，被测对象改变，即用同一台仪器对同一批零件进行n件（或n组）测量，根据测量结果计算出 σ，以便进行工艺调整，尤其对特殊精密加工设备大修后的考核。除按规程经机修检验外，一般都要试加工零件。送计量室，给出结论。这里就不能以一两件零件来评定，而应重复加工数件，用确定修后结果。

当被测零件（或参数）精度特别高，又无更高精度的仪器可供选择，而在已有的几台同类仪器上分别测量时。其结果差异又较大（仪器均合格），则可对几台仪器进行等精度检定，分别计算出各自的σ值。在别无选择的情况下，即可选其中σ最小的一台用于该零件的测量。

当对一批测量值供需双方有争议，又不便对提出异议方的实物进行复测时，则可从被诉方同一批尚存的样件中抽取n个子样进行复测（或从原记录中抽取n个数值）计算出σ值（为慎重，可同时复核一下计量器具的合格性），再根据对方提供的数据算出σ1值。如果被诉方的计量器具合格，且选择符合误差要求，当出现 σ1>>σ 时，即可断定σ1方的测量不准。利用这种分析方法可避免盲目退货或盲目派员处理。如宝钢就曾用此方法处理一起涉外争议：一批出口钢坯，对方提出异议，他们在确认计量器具合格的基础上，从未发出的同一批中抽取32件进行复测，算出σ=0.03，据对方提供的数据算出σ1=0.21，σ1>> σ，因此确认对方测量有误。对方终于接受了宝钢的结论，撤销了异议2。