[科普中国]-解耦算法

解耦思想的提出

在多变量系统中，由于被控对象各个通道之间相互铰链，一个输入信号的变化会引起多个输出量的变化，每个输出也不止受一个输入的影响，系统的这种相互关联称之为藕合，在存在着耦合的系统中，即使精心选择输出与控制输入之间的配对关系，也难免存在相关现象，所以使输出独立地跟踪各自的设定值有一定困难。这时，再设计相应的控制器来跟踪系统的输入就比较容易了。解耦控制的思想最早是由Gilbert E.G.完成的。当时称为Morgan问题。解耦问题是多输入多输出(MIMO)线性定常系统综合理论的一个重要组成部分。其目的是寻找合适的控制规律使闭环控制系统实现一个输出分量仅仅受一个输入分量控制，而且不同的输出分量受不同的输入分量控制，从而可以运用经典的控制系统综合方法进行系统校正，以使系统的动静态性能及各项指标满足工程需要1。

解耦方法分类根据解耦的程度，解耦可分为全解耦和近似解耦；根据解耦的时间特性，解耦又可分为静态解耦和动态解耦。对于确定的线性多变量系统，可采用对角矩阵法，相对增益分析法，反Nyquist曲线法，特征曲线分析法，状态变量法，序列回差法等传统的解耦方法进行控制。但是复杂工业过程中的系统存在着多变量、强耦合、非线性、动态特性变化大、生产工况变化频繁等情形，这时传统的解耦方法就不适用了，因而产生了新的多变量解耦控制方法。将自适应控制、模糊控制与解耦控制相结合并用于多变量系统中，就形成了多种解耦控制方法2。

传统解耦方法传统解耦方法以现代频域法为代表，也包括时域方法，主要适用于线性定常多输入多输出系统。

自适应解耦方法自适应控制的思想与解耦技术相结合并用于多变量系统中，就形成了自适应解耦方法。自适应解耦的目标是使系统的闭环传递函数成为对角阵，通常把耦合信号作为干扰处理。自适应解耦实质上采用了最优控制的方法，建立目标函数并对参数寻优是该方法的核心，这是与传统解耦方法的本质区别，是解耦理论的重大突破，同时也是智能解耦理论的基础。自适应解耦可适用于时变对象。

智能解耦方法智能解耦方法以神经元网络解耦方法为代表。由于神经网络可实现多输入到多输出的映射，以任意精度逼近任意函数，并具有自学习功能，因此适用于时变、非线性、特性未知的对象3。

解耦算法选择适当的控制规律将一个多变量系统化为多个独立的单变量系统的控制问题。在解耦控制问题中，基本目标是设计一个控制装置，使构成的多变量控制系统的每个输出变量仅由一个输入变量完全控制，且不同的输出由不同的输入控制。

解耦原理对于输出和输入变量个数相同的系统，如果引入适当的控制规律，使控制系统的传递函数矩阵为非奇异对角矩阵，就称系统实现了完全解耦。使多变量系统实现完全解耦的控制器，既可采用状态反馈结合输入变换的形式，也可采用输出反馈结合补偿装置的形式。

已证明，系统可用状态反馈和输入变换，即通过引入控制规律u=-Kx+Lv，实现完全解耦的充分必要条件是矩阵E为非奇异。这里，u为输入向量，x为状态向量，v为参考输入向量，K为状态反馈矩阵，L为输入变换矩阵。对于满足可解耦性条件的多变量系统，通过将它的系数矩阵A，B，C化成为解耦规范形，便可容易地求得所要求的状态反馈矩阵K和输入变换矩阵L。完全解耦控制方式的主要缺点是，它对系统参数的变动很敏感，系统参数的不准确或者在运行中的某种漂移都会破坏完全解耦。

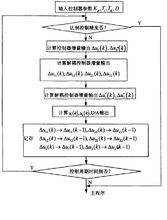
算法流程图解耦控制算法流程图如图所示4。