[科普中国]-算子模糊逻辑

发展过程

自从1965年Zadeh教授提出Fuzzy集理论后；Fuzzy逻辑及其Fuzzy推理就成为计算机科学家们感兴趣的问题，井逐渐被承认为人工智能理论基础中一个重要组成部份。2

1971年Lee和 Chang提出了建立在[0,1]区间上的 Fuzzy 逻辑，井将归结方法引入Fuzzy逻辑做为一种反向 Fuzzy推理规则。2

1975年Zadeh提出了模糊语言逻辑和给出了一种正向 Fuzzy推理规则。2

1980年刘叙华教授根据模糊语言逻辑中的 Fuzzy命题的真值是取在由Fuzzy集组成的格上的特点，建立了真值取在格上的 Fuzzy逻辑，并将归结方法引人该逻辑 ，得到一种反向 Fuzzy 推理规则。

Zadeh的模糊语言逻辑是建立在崭新的语言变量这个概念上，由于它紧紧抓住了语言模糊这个本质现象，因此这个逻辑系统表现出丰富的内涵，但是， 该系统提出的对于程度词的处理还是初步的。2

刘叙华教授提出的格上的 Fuzzy 逻辑，虽然是比模糊语言逻辑更为一般的抽象，但是由于这种数学上的抽象，使得该系统不能明晰的显现 Fuzzy命题和Fuzzy推理的特点，因为该系绕对Fuzzy命题的描写，在形式上和二 值逻辑对普通命题的描写没有区别，Fuzzy 命题与普通命题的唯一区别隐藏在原子的真值里。2

因此，1984年刘叙华教授等人提出了一种所谓“算子Fuzzy逻辑”的概念。在这种系统里，一个Fuzzy命题中的所有程度词，都可明晰的用算子表示出来，这种表示方式，在形式上有点类似著名专家系统MYCIN 中的知识和规则。将归结方法引人这个系统，得到了所谓2一归结方法。引进了一个定理的λ一恒真和λ一恒假的概念， 亦即，不仅能描述一个Fuzzy定理，而且能描述这个Fuzzy 定理能在多大程度上成立的模糊程度。λ一归结方法做为反向 Fuzzy推理规则，能够反证任何一个在算子Fuzzy逻辑系统中，任意一个 λ一恒假的 Fuzzy定理。2

算子模糊逻辑的概念在OFL系统中：

( l ) 文字具有形式λ1…λnP，其中λ1是算子，P是二值逻辑中的原子，故OFL 中公式的解释和二值公式的解释相同；

( 2 ) 一般地λ1…λnP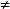 (λ1·λ2·…·λn)P；

( 3 ) 算子格中的运算·，可以取做算术平均值运算。3

由于在OFL系统中，λ1…λnP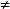 (λ1·λ2·…·λn)P ，因此，在OFL中引进归结原理时便遇到麻烦。另外，将算子运算理解为证据的积累似为合理，基于这些考虑，刘叙华教授于1990年 7 月对原 OFL 系统作了改进（我们称为狭义算子模糊逻辑），并且提出了结合算子格、α——解释及λα——恒假的概念。狭义算子模糊逻辑是建立在特殊结合 算子格([0,1] , ≤)上的。3.