[科普中国]-模板匹配

模板就是一副已知的小图像，而模板匹配就是在一副大图像中搜寻目标，已知该图中有要找的目标，且该目标同模板有相同的尺寸、方向和图像元素，通过一定的算法可以在图中找到目标，确定其坐标位置。1

以8位灰度图像为例，模板T(m,n)叠放在被搜索图S(W,H)上平移，模板覆盖被搜索图的那块区域叫子图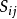 ，i,j为子图左下角在被搜索图S上的坐标，搜索范围是：1≤i≤W-n，1≤j≤H-m。可以用下式衡量T和 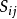的相似性：

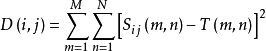
将其归一化，得模板匹配的相关系数：

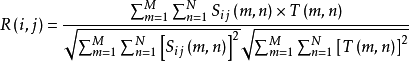当模板和子图一样时，相关系数R(i,j)=1，在被搜索图S中完成全部搜索后，找出R的最大值 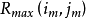，其对应的子图 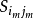即为匹配目标。显然，用这种公式做图像匹配运算量最大、速度最慢。1

误差法即衡量T和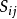 的误差，其公式为：

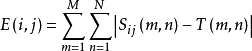
其中E(i,j)为最小值处即为匹配目标。为提高计算速度，取一误差阈值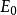 ，当E(i,j)> 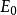时便停止该点的计算，继续计算下一点。

模板越大，匹配速度越慢；模板越小，匹配速度越快。1

二次匹配误差算法中匹配分两次进行。

第一次匹配是粗略匹配。取模板的隔行隔列数据，即四分之一的模板数据，在被搜索图上进行隔行隔列扫描匹配，即在原图的四分之一范围内匹配。由于数据量大幅度减少，匹配速度显著提高。

误差阈值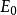 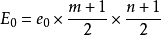： ，其中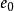， 为各点平均的最大误差，一般取40~50即可；m,n分别为模板的长和宽。

第二次匹配是精确匹配。在第1次误差最小点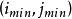 的领域内，即在对角点为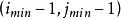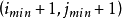，的矩形内进行搜索匹配，得到最后结果。实验结果表明，二次匹配误差法的速度比其他算法快10倍左右。1

与边缘检测中使用的模板不同，模板匹配中使用的模板相当于（8×8~32×32）。从大幅面图像寻找与模板最一致的对象，计算量大，要哦花费相当多的时间。为使模板匹配高速化，Barnea等人提出了序贯相似性检——SSDA法（sequential similiarity detection algorithm）。2

SSDA法计算图像f(x,y)在像素（u,v）的非相似度m(u,v)为：

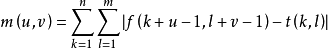以m(u,v)作为匹配尺度。式中（u,v）表示的不是模板与图像重合部分的中心坐标，而是重合部分左上角像素坐标。模板的大小为：n×m。

如果在图像（u,v）处有和模板一致的图案，则m(u,v)值很小，相反则较大。特别是在模板和图像重叠部分完全不一致的场合下，如果在模板内的各像素与图像重合部分对应像素的差的绝对值依次增加下去，其和就会急剧地增大。因此，在做加法的过程中，如果差的绝对值部分和超过了某一阈值时，就认为这位置上不存在和模板一致的图案，从而转移到下一个位置上计算m(u,v)。由于计算m(u,v)只是加减运算，而且这一计算在大多数位置中途便停止了，因此能大幅度地缩短计算时间，提高匹配速度。2

还有一种把在图像上的模板移动分为粗检索和细检索两个阶段进行的匹配方法。首先进行粗检索，它不是让模板每次移动一个像素，而是每隔若干个像素把模板和图像重叠，并计算匹配的尺度，从而求出对象物大致存在的范围。然后，在这个大致范围内，让模板每隔一个像素移动一次，根据求出的匹配尺度确定对象所在的位置。这样，整体上计算模板匹配的次数减少，计算时间短，匹配速度就提高了。但是使用这种方法存在漏掉图像中最适当位置的危险性。2

一般的图像中有较强的自相关性，因此，进行模板匹配计算的相似度就在以对象物存在的地方为中心形成平缓的峰。这样，即使模板匹配时从图像对象物的真实位置稍微离开一点，也表现出相当高的相似度。上面介绍的粗精检索高速化恰好利用了这一点。但为了求得对象物在图像中的精确位置，总希望相似度分布尽可能尖锐一些。

为了达到这一目的，人们提出了基于图案轮廓的特征匹配方法。图案轮廓的匹配与一般的匹配法比较，相似度表现出更尖锐的分布，从而利于精确定位。2

一般来说，在检测对象的大小和方向未知的情况下进行模板匹配，必须具备各式各样大小和方向的模板，用各种模板进行匹配，从而求出最一致的对象及其位置。2

另外，在对象的形状复杂时，最好不把整个对象作为一个模板，而是把对象分割成几个图案，把各个分图案作为模板进行匹配，然后研究分图案之间的位置关系，从而求图像中对象的位置。这样即使对象物的形状稍微变化，也能很好地确定位置。2

在应用模板匹配法进行图像匹配时，应注意以下几点：
　　（1）归一化互相关注进行匹配，模板应在（M-P+1）×（N-Q+1）个参考位置上进行相关计算，计算量非常大，必要时可以采用序贯相似检验算法、幅度排序相关算法、FFT相关算法、分层搜索序贯判决等方法对其进行改进，以提高运算速度。

（2）模板匹配具有自身的局限性，主要表现在它只能进行平行移动，若原图像中的匹配目标发生旋转或大小变化，该算法无效。

（3）若原图像中要匹配的目标只有部分可见，该算法也无法完成匹配。3