算法复杂性分析(Algorithm complexity analysis)主要是针对运行该算法所需要的计算机资源的多少。当算法所需要的资源越多,该算法的复杂性越高;反之,当算法所需要的资源越少,算法的复杂性越低。
对于任意给定的一个问题,设计出复杂性最低的算法是在设计算法时追求的重要目标之一;而当给定的问题存在多种算法时,选择其中复杂性最低的算法是选用算法时遵循的重要准则。因此,算法的复杂性分析对算法的设计或选用具有重要的指导意义和实用价值。
工作原理时间复杂度通常,对于一个算法的复杂性分析主要是对算法效率的分析,包括衡量其运行速度的时间效率及衡量其运行时所需要占用空间大小的空间效率。
对于早期的计算机来说,时间与空间都是极其珍贵的资源。由于硬件技术的发展大大提高了计算机的存储容量,使得存储容量的局限性对于算法的影响大大降低。但是时间效率并没有得到相应程度的提高。因此,算法的时间效率或算法时间复杂度是算法分析中的关键所在。
对于算法的时间效率的计算,通常是抛开与计算机硬件、软件有关的因素,仅考虑实现该算法的高级语言程序。一般而言,对程序执行的时间复杂度的分析是分块进行的,先分析程序中的语句,再分析各程序段,最后分析整个程序的执行复杂度。通常以渐进式的大O形式来表示算法的时间复杂度。渐进式的大O形式表示时间复杂度的主要运算规则有如下2种。
(1)求和规则
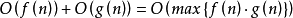 其中,
其中,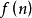 和
和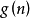 表示与
表示与 个有关的一个函数。
个有关的一个函数。
(2)乘法规则
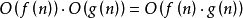
 ,c是一个正数。
,c是一个正数。
假设 是问题规模
是问题规模 (
( 为整数)的函数,算法的时间复杂度可以定义为
为整数)的函数,算法的时间复杂度可以定义为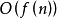 ,记作:
,记作:
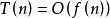 由于随着问题规模
由于随着问题规模 的增长,算法执行时间的增长率和
的增长,算法执行时间的增长率和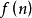 的增长率相同,因此
的增长率相同,因此 也被称为算法的时间复杂度。
也被称为算法的时间复杂度。
为了便于比较同一问题的不同算法的效率问题,通常的做法是从算法中选取一种对于所研究问题来说是基本运算的原子操作,以该基本操作重复执行的次数作为算法的时间度量单位。
空间复杂度一般情况下,一个算法所占用的存储空间包括算法自身、算法的输入、算法的输出及实现算法的程序在运行时所占用空间的总和。
由于算法的输入和输出所占用的空间基本上是一个确定的值,它们不会随着算法的不同而不同。而算法自身所占用的空间与实现算法的语言和所使用的语句密切相关,例如程序越短,它所占用的空间就越少。一个算法在运行过程中所占用的空间,特别是算法临时开辟的存储空间单元则是由算法策略及该算法所处理的数据量决定的。因此对于一个算法的空间复杂度的衡量主要考虑的是算法在运行过程中所需要的存储空间的大小。
 假设
假设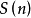 是问题规模
是问题规模 (为整数)的函数,可以定义算法的空间复杂度为
(为整数)的函数,可以定义算法的空间复杂度为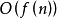 ,记作:
,记作:
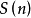 =
=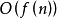
与时间复杂度 一样,
一样,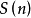 也被称为算法的空间复杂度。1
也被称为算法的空间复杂度。1




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国