[科普中国]-模糊逻辑系统

工作原理纯模糊逻辑系统

纯模糊逻辑系统是其他类型的模糊逻辑系统的核心部分，它提供了一种量化语言信息和在模糊逻辑原则下利用这类语言信息的一般化模式，其基本框图如图2-1所示。

纯模糊逻辑系统也可以解释为一个映射关系，其结构图中的中间部分具有类似于（代数学中）线性变换中变换矩阵的映射功能，输入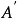映射为输出，即有=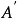。R。纯模糊逻辑系统的缺点就在于它的输入和输出均为模糊集合，这不利于工程应用。但是，它为其他具有应用价值的模糊逻辑系统提供了一个基本的样板，由此出发可以构造出其他具有实用性质的模糊逻辑系统。

高木-关野模糊逻辑系统高木-关野模糊逻辑系统（简称T-S模糊逻辑系统）是将纯模糊逻辑系统中的每一条模糊规则的后件（即THEN以后的部分）加以定量化后形成的，也就是说，T-S模糊逻辑系统中的模糊规则，其前件是迷糊的，后件是确定的。

高木-关野模糊逻辑系统结构图如2-2所示。这种模糊逻辑系统已经在许多实际问题中得到成功的应用，它的优点是模糊逻辑系统的输出为精确值，其中的参数也可以用参数估计、适应机构等方法加以确定。但是，由于模糊规则后件的确定性，T-S模糊逻辑系统不能方便地利用更多的语言信息和模糊原则，限制了其应用的灵活性。

具有模糊产生器及模糊消除器的模糊逻辑系统具有模糊产生器及模糊消除器的模糊逻辑系统的基本框图如图2-3所示。它是把纯模糊逻辑系统的输入端和输出端分别接上模糊产生器和模糊消除器后构成的。

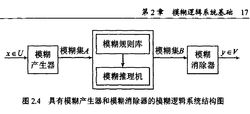
具有模糊产生器及模糊消除器的模糊逻辑系统具有以下三方面的显著优点：（1）这种模糊逻辑系统为我们提供了一种描述领域专家知识的模糊规则的一般化方法；（2）使用者在设计其中的模糊产生器、模糊推理机和模糊消除器时具有很大的自由度，因此可以根据实际情况，找到一个最适合的模糊逻辑系统；（3）因为其输入、输出均为精确值，因此特别适合在工程领域中应用。所以，这类模糊逻辑系统得到了更广泛的应用，特别是当采用单点模糊化、乘积推理、中心解模糊和高斯型隶属函数构造这种系统时，其输出可以逼近有界闭集上任意给定的连续函数。

这种模糊逻辑系统是由Mamdani首先提出，而且已经在许多工业过程和商业产品中得到成功的应用。1