[科普中国]-逐步排序j检验

定义

逐步排序检验是每次呈给评价员一对样品，随机给出。评价员需要回答的问题是“哪个样品更甜(酸)”。评价组的每一个评价员将所有可能的成对样品全部评定。结果用结果用Friedman秩和检验分析的的一种感官检验方法。1逐步排序检验是比较数个样品某种感官性状的强度差异的一种食品感官检验方法，属于多样品性质差别检验的一种。

应用领域和范围

这一方法是对几个样品的某个特定性质的比较测定，特别适用于3～6个品的感官检验，可以用相对经验较少的评价员评定。

特点

逐步排序检验提供的样品条件要尽量一致，包括大小、容器、温度等。试验时，采用均衡随机的顺序将样品呈送给品评员，每次只提供给评价员一对样品。有必要利用有色光源，如绿、蓝或红，将原有样品的颜色加以掩饰。当然，被检验的特征就是要对颜色进行检验，那么必须用白色光源。

逐步排序检验可以比较多个样品间某一特定感官性质(如甜度、风味强度等)强度次序，操作简单，受记忆力影响较小。

逐步排序检验的缺点是只要能排出样品强度次序，不评价样品间差异程度的大小，两个位置相邻的样品无论差别非常大还是仅有细微差别，都是以一个秩次单位相隔；不适用与样品数量较多（大于6个）的感官检验，当比较样品增多，要求比较的样品数目很大，甚至无法比较。2

评价员

评价员可以进行较少的培训，指导同三点测定。用10个以上的评价员，如果用30个或更多的评价员区别能力可以大大改善。保证所有评价员对所评性质均能识别。

样品准备与呈送

检验的产品控制等同三点检验。首先是实验分组：如评价元为30人，每10人为1组，则分3个小组，每组选出1个小组长，轮流进入实验区。然后是利用随机数表或计算机品评系统对样品进行编码，编码实例，如需重复检验时，可给每个样品3个编码。样品呈送时，可以同时或分别给出样品。但必须保证样品的给出次序是完全随机的，每一对的两个样品、各样品对以及评价员之间均应随机。试验前，主持人向品评员说明检验的目的，并组织对检验方法、判定准则进行讨论，使每个品评员对检验的准则有统一的理解。根据要求，在限定时间内埘所供样品依次进行品评。评价员必须回答样品间指定的某一感官特性“哪个样品更强？”，不允许有“无差异”的回答存在。

结果整理与分析1

①计算各样品的秩次和。

②Friedman秩和检验采用Friedman秩和检验分析评价的几个样品感官性质是否有显著性差异。Friedman F统计量：

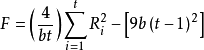式中：b —— 评价员数量

t —— 样品数量

Ri—— 样品 i 的秩次和

比较的临界值可以查Friedman秩和检验临界值表，如果b、t较大，表中没有相应的临界值，则将F值与自由度为(t-1)的比较。

通过Friedman秩和检验，如果没有显著性差异，即可直接得出样品问没有显性差异的推论；如果有显著性差异，再采用Tukey’sHSD法比较哪些样品问有差异。

③样品间的比较查q表，在显著性水平为d、k=t、自由度为∞时的q值，按照下式计算比较的临界值HSD：

HSDα=qα,t,∞×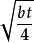

然后将各样品的秩次和差与计算的临界值HSDα比较，如果差值大于等于HSDα，则表明比较的两个样品问有显著性差异。

应用实例

食用玉米糖浆生产者希望生产固形物一定、但橱度低的混和玉米糖浆。现有4个未调味的玉米糖浆混和物A、B、C、D，对其稠度进行评价，以确定适宜规模生产的产品。试验采用逐步排序检验，选12个有识别能力的评价员评定6组所有可能的样品对：AB、AC、AD、BC、BD、CD。评定结果见下表，表中数字为每一样品对判断为更强的人数，如C和B，有6人认为C比B强，相应有6人认为B比C强。试分析各样品间稠度是否有差异。

4个玉米逐步排序检验结果

|| ||

计算秩次和：在本例中，在每组成对样品中校选为更稠(排在第一)的样1品给秩“l”，被评为更稀(排在第二)的样品给秩“2”，计算每个样品的秩和。如样品B有两组数据；B行的数据表示样品B与其他样品进行成对比较时，样品B被评价为更稠的评价员数量，此时样品B在BA、BC、BD样品对中分别有12、6、2个评价员评定B比另一样品更稠(即在这些样品对中，样品B排第一，更稠)，因此其秩和1*(12+6+2)=20；B列的数据表示样品B与其他样品进行成对比较时，样品B被评价为更稀的评价员数量，此时样品B在BA、BC、BD样品对中分别有0，6，10人评定B更稀(即在这些样品对中，样品B排第二，更稀)，因此其秩和为：2x(0+6+10)=32；样品B总秩次和为助20+32=52。其他样品秧和计算方法相同，结果如下：

样品 A B C D

秩次和（Ri）： 71 52 48 45

计算friedman 分析:

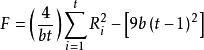
=（4/12×4)(71+52+48+45)-9×12×(4-1)

=34.17

查自由度df= t-1 = 4-1 =3的χ2表得：

χ20.05（3）=7.81 ； χ20.01（3）=11.34

计算出的F=34.17，比χ20.01（3）大，因此几个样品的稠度有极显著差异。

各样品间稠度的比较 查q表（见附表3），k=t=4，α=0.05时得到

qα,t,∞= q0.05,t,∞=3.63，有：

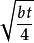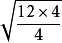HSD0.05= qα,t,∞ ×=3.63=12.6

则：RA -RB =71-52=19﹥HSD0.05=12.6，因此，样品A与样品B问稠度有显著差异。同样，进行其他样品间的比较，最后得到样品A显著地比样品B、C、D淡，所以说A的稠度最低，与其他几个样品问有显著性差异，而B、C和D的稠度差异不显著。