[科普中国]-概率分布评估模型

概述

点评估模型无法对评估对象得出准确的暴露评估，这就需要更准确的膳食暴露评估。这些精确包括得到更多关于食品被消费的详细资料或采用更复杂的膳食暴露评估模型从而切合实际地模拟消费者行为。

对那些需要在筛选方法或点暴露评估方法外还需进一步精确的数据，可使用概率分析法对暴露变异性加以分析。从概念上讲，人群暴露情况一般被人为是一个值域，而非一个点值，因为人群的每个人在经历着不同的暴露水平。造成人群暴露差异的变异性因素包括年龄、性别、种族、国籍和地区、个人爱好等，膳食暴露中的变异性经常被用“概率分布”进行表述，有时，频率分布近似于连续概率分布。

变异性分布以其代表性的人群数量为为特点，比如个人中值暴露位于分布曲线的中间，其95%个人位点的暴露值，是指其超过人群每100人中95人的暴露水平。“平均”或是“中值’暴露不一定代表任何特殊的个人情况。相反，平均暴露是通过加和所有个人的暴露量然后除以整体人群数量而得到的。

概率模型概率评估模型应对不同情况有4 种主要方法: 简单分布评估、随机抽样评估、分层抽样评估和拉丁超立方抽样评估。其中简单分布估计主要是由食品消费调查得到的食品消费量的经验分布和相应食品中化学物质浓度的点评估相乘即可得到暴露量分布; 分层抽样是指将食品消费分布和化学物质浓度分为若干层。四种方法是根据不同情况来使用。

概率评估模型是:

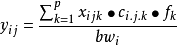
式中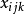表示第i个个体在j天摄入第k种食品的量，一般来源于全国膳食调查，而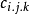表示一般来源于市场上各种食品的残留检测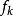，表示食品的加工因子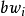，表示观察个体i的体重。1

从概率评估的角度，是分别将从食品摄入量和化学物的浓度作为总体A和B，在获得A 和B两总体独立的分布特征和相应的总体参数后，进行抽样获得yij的概率分布，从而得到平均值，P50，P90，P97. 5，P99 作为目标人群的摄入量评估值。根据上述得到的概率分布，利用统计模拟方法产生一系列描述结果参数的统计分布，评价污染物的急性摄入风险。它的优点在于可以对不确定性进行全面分析，可以作为一种模型产生的假设结果，它是一种更精确的膳食暴露评估，暴露评价结果较真实且不确定性较小; 缺点是费用较高，较难大范围实施。

简单分布评估膳食暴露评估可基于食品消费量的分布。这一分布可通过经验由食品消费调查和一个能代表相关食品商品化学物浓度的简单点评估确定。食品消费分布曲线上的每一个点值可乘以相关食品商品中的化学浓度值。反过来说，食品消费也可能有一个点评估，即这一食品中化合物浓度也有一个经验分布。因此，最终就有可能有足够的数据同时确定食品消费数量和食品化学物水平的分布概况。

随机抽样评估由食品消费量和化合物浓度分布的随机抽样评估的方法需数据集能够表征每一相关食品中化合物浓度分布情况，同时还要能表征所关注人群对同一食品的消费分布情况。这一方法明确考虑了输入数据的变异性，对简单的确定性评估方法而言其提供了更贴合实际的结果，因为在简单的确定性评估中，当选择一个单一值以表征整个分布情况时，方法通常受限于其保守的默认假设。

蒙特卡罗迭代涉及涉及使用随机数来选择输入分布的值。这一技术已被应用于各种不同的模拟方案中，在恰当使用时，其结果将会模拟实际情况，因为这一技术所使用的值均在每一数据分布范围内。2

由于是随机抽样，因此，蒙特卡罗模拟可能在其分布极端（高端、低端）时将会不准确，当在使用参数分布而不是非参数（经验）分布数据时尤其如此。在这种情况下，当对污染数据使用非参数方法时，那么对其分布尾端的临界值，及所选食品的”现实“最大观测值，可引入非参数方法从而避免将现实生活中永远不会发生的”不现实“污染事件纳入模型中。

分层抽样评估分层抽样方法为每一分布选择等距值。例如，确定每一分布的平均数或其四分位点中值。单个分层计算的主要缺点是没有极值评估。通过使用多层方法（如估计每一十分位平均值而不是每一四分位值）可改善此问题，但不能完全克服。通过使用多层方法可得到详尽、准确及重现性好的输出分布。分层抽样的难点是需要迭代的次数可能会变得非常大，并且可能需要额外的计算机软件技术。

拉丁超立方抽样拉丁超立方抽样是统计学方法，实质上是一种分层和随机的混合抽样方法。首先将分布分层，之后由每层随机抽样，从而确保在每一浓度和食品消费量数据分布范围内的迭代平衡，另外，这种方法还允许一些样品得出的极端分布值。