简介
数学上,高斯消元法(或译:高斯消去法),是线性代数规划中的一个算法,可用来为线性方程组求解。但其算法十分复杂,不常用于加减消元法,求出矩阵的秩,以及求出可逆方阵的逆矩阵。不过,如果有过百万条等式时,这个算法会十分省时。一些极大的方程组通常会用迭代法以及花式消元来解决。当用于一个矩阵时,高斯消元法会产生出一个“行梯阵式”。高斯消元法可以用在电脑中来解决数千条等式及未知数。亦有一些方法特地用来解决一些有特别排列的系数的方程组1。
Gauss-Jordan消元法在很多地方都会用到,例如求一个矩阵 的逆矩阵、解线性方程组,等等。它的速度不是最快的,但是它非常稳定, 同时它的求解过程也比较清晰明了, 因而人们使用较多。相对于高斯消元法,Gauss-Jordan消元法最后的得到线性方程组更容易求解,它得到的是简化行列式。其转化后的增高矩阵形式如图1所示,因此它可以直接求出方程的解,而无需使用替换算法。但是,此算法的效率较低。
的逆矩阵、解线性方程组,等等。它的速度不是最快的,但是它非常稳定, 同时它的求解过程也比较清晰明了, 因而人们使用较多。相对于高斯消元法,Gauss-Jordan消元法最后的得到线性方程组更容易求解,它得到的是简化行列式。其转化后的增高矩阵形式如图1所示,因此它可以直接求出方程的解,而无需使用替换算法。但是,此算法的效率较低。
G-J消元法的初等变换方法G-J 消元法通过这样的方法来进行初等变换:在每一个循环过程中,先寻找到主元,并将主元通过行变换 (无需列变换) 移动到矩阵的主对角线上, 然后将主元所在的行内的所有元素除以主元,使得主元化为 1;然后观察主元所在的列上的其他元素,将它们所在的行减去主元所在的行乘以一定的倍数, 使得主元所在的列内、 除主元外的其他元素化为 0,这样就使得主元所在的列化为了单位矩阵的形式。 这就是一个循环内做的工作。 然后, 在第二轮循环的过程中, 不考虑上一轮计算过程中主元所在的行和列内的元素, 在剩下的矩阵范围内寻找主元, 然后(如果其不在主对角线上的话) 将其移动到主对角线上, 并再次进行列的处理, 将列化为单位矩阵的形式。 余下的步骤依此类推。 具体的计算过程的一个例子, 请看下面求逆矩阵的过程的例子。
Gauss-Jordan 法的求解方程组的过程引例假设有如下的方程组:
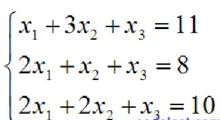
写成矩阵形式就是: AX=B ,其中:
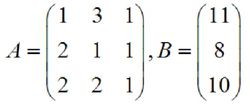
且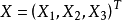 ,现对矩阵 A 作初等变换,同时矩阵 B 也作同样的初等变换,则当 A 化为单位矩阵的时候,有:
,现对矩阵 A 作初等变换,同时矩阵 B 也作同样的初等变换,则当 A 化为单位矩阵的时候,有:
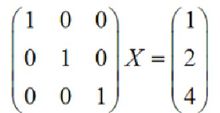
显而易见,我们得到了方程组的解: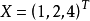 。
。
所以, 我们要以一定的策略, 对 A 和 B 施以一系列的初等变换, 当 A 化为单位矩阵的时候,B 就为方程组的解。
求解过程如果要解系数矩阵相同、右端向量不同的 N 个方程组,在设计程序的时候,没有必要 ”解 N次方程组 “,我们完全可以在程序中,将所有的右端向量以矩阵的数据结构(类似于二维数组)来表示, 在系数矩阵作行变换的时候, 矩阵里的每一个右端向量也做同样的变换, 这样,我们在一次求解运算的过程中,实际上就是同时在解 N 个方程组了。
用G-J消元法求逆原理假设 AX=E ,其中, A 为 n 阶系数矩阵(与上面的解线性方程组对照);E 为单位矩阵,即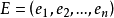 ,其中
,其中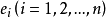 为单位列向量; X 为 n 个列向量构成的矩阵,即
为单位列向量; X 为 n 个列向量构成的矩阵,即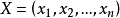 ,其中
,其中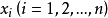 为列向量。于是,可以把等式 AX=E 看成是求解 n 个线性方程组
为列向量。于是,可以把等式 AX=E 看成是求解 n 个线性方程组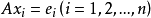 ,求出了所有的
,求出了所有的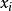 之后,也即得到了矩阵 X。而由 AX=E 可知,矩阵 X 是 A 的逆矩阵,即
之后,也即得到了矩阵 X。而由 AX=E 可知,矩阵 X 是 A 的逆矩阵,即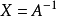 。这样,就求出了 A 的逆矩阵了。于是,求逆矩阵的过程被化成了解线性方程组的过程,因此我们可以用 Gauss-Jordan 消元法来求逆矩阵。求逆矩阵时,系数矩阵 A 和单位矩阵 E 可以共用一块存储区,在每一次约化过程中,系数矩阵逐渐被其逆矩阵替代。
。这样,就求出了 A 的逆矩阵了。于是,求逆矩阵的过程被化成了解线性方程组的过程,因此我们可以用 Gauss-Jordan 消元法来求逆矩阵。求逆矩阵时,系数矩阵 A 和单位矩阵 E 可以共用一块存储区,在每一次约化过程中,系数矩阵逐渐被其逆矩阵替代。
示例有如下的方程组:
显而易见,该方程组对应的系数矩阵 A 和右端向量矩阵 B(此处只有一个右端向量)分别为:
其实在求逆矩阵的过程中,矩阵 B 无关紧要,可以忽略,不过此处还是把它写出来了。下面,把单位矩阵 E 附在 A 的右边,构成另一个矩阵(A|E):

下面,通过矩阵的初等变换,将 A 化为单位矩阵 E,而 E 则化为了 A 的逆矩阵。以下是转化步骤:
(1)主元选为 3,所以将 Row1 (第一行)与 Row2 (第二行)交换:

(2)主元所在行的所有元素除以主元:

(3)Row1 – Row2 ,Row3 – 2 × Row2 :

现在,原来的矩阵 A 有一列被化为了单位阵的形式。
(4)重新选主元,这一次主元选为 5/3,于是 Row1 ÷ 5/3 (主元所在行的所有元素除以主元):

(5)Row2 – (1/3) × Row1 ,Row3 – (4/3) × Row1 :
现在,原来的矩阵 A 又有一列被化为了单位阵的形式。
(6)重新选主元,这一次主元选为 -1/5 ,于是 Row3 ÷ (-1/5) (主元所在行的所有元素除以主元):
(7)Row1 – (2/5) × Row3 ,Row2 – (1/5) × Row3 :

现在,原来的矩阵 A 的所有列都被化为了单位阵的形式。可见,以上过程非常适合于计算机编程求解。至此,我们完成了从 A 到 E 的转换,这个过程中使用了选主元的方法,但没有使用列交换。于是,原来的单位矩阵 E 就变成了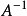 ,即:
,即:




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国