[科普中国]-库埃特流动

简介

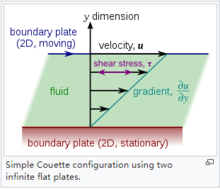
库埃特流动是指粘性流体在相对运动着的两平行平板之间的层流流动。1在流体动力学中，库埃特流动是两个表面之间的空间中粘性流体的流动，其中一个流体相对于另一个表面正切向移动，通常采取两个平行板的形式或两个同心圆筒之间的间隙的形式。库埃特流动是由作用在流体上的粘性力和与平板平行的外部压力推动的。这种流动类型是为了纪念 Maurice Marie Alfred Couette而命名的，他是19世纪末法国安格斯大学的一位物理学教授。

Couette配置模拟了一些实际问题，如轻载轴颈轴承中的流动，并且经常用于粘度计并显示可逆性的近似值。聚合物流体在流动中，由于边界的运动而带动流体流动。例如用同轴圆筒式勤度计测量勃度时，流体除了因圆筒的相对运动导致两圆筒间环形流休的剪切流动外，还由于圆筒的旋转而带动流体的拖曳流动。此外，在聚合物的挤出成型(螺杆为运动边界)和电缆线包覆层成型(金属电线为运动边界)等成型工艺中，均可产生库埃特流动。在成型设备的设计和工艺条件的控制中对这种流动要加以考虑。

平面库埃特流动Couette流量通常用于本科物理和工程课程，以说明剪切驱动的流体运动。最简单的概念是找到两个无限的平行板，距离为h。 一个平板，以一个恒定的速度U在自己的平面中平移。 2忽略压力梯度，Navier-Stokes方程简化为

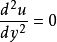
其中y是与板垂直的空间坐标，u（y）是速度分布.该方程式反映了流量是单向的假设。也就是说，三个速度分量（u，v，w）中只有一个是不平行的。 如果y起源于下板，边界条件为u（0）= 0和u（h）= U。确切的解决方案为

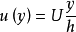
可以通过对边界条件的两次积分来求解。流动的一个显著方面是剪切应力在整个流动区域是恒定的。特别地，速度的一阶导数 U / h是常数。根据牛顿粘度定律（牛顿流体），剪切应力是该表达式与（恒定）流体粘度的乘积。

库埃特流动启动实际上，库埃特流动解决方案无法立即实现。 启动问题由下式给出：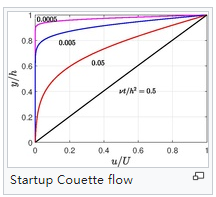

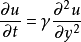初始条件为

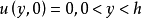边界条件为

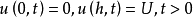
通过减去稳定解和使用变量分离，可以将问题转化为均匀问题，解决方案为

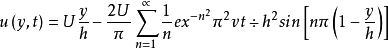
当t 时，稳定的库埃特流动得以恢复，甚至可以达到稳定的库埃特流动。如图所示，达到稳定所需的时间仅取决于板材间的间距h和流体的运动粘度，但不限于顶板移动速度U的快慢。

库埃特流动与压力梯度当平行的方向施加恒定压力梯度G=-dp/dx时，会出现更一般的库埃特流动情况。 在这种情况下，Navier-Stokes方程简化为

其中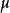 是流体粘度。 将上述等式两次积分并应用边界条件（与没有压力梯度的Couette流动相同），得到以下精确解为

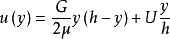
压力梯度可以是正的（不利的压力梯度）或负的（有利的压力梯度）。 可以注意到，在固定板即 U = 0的限制情况下，流被称为具有对称（相对于水平中平面）抛物线速度分布的平面Poiseuille流。

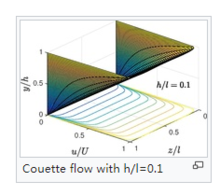
库埃特流动与矩形通道当两个平板在流向x和展开方向 z方向上无限长时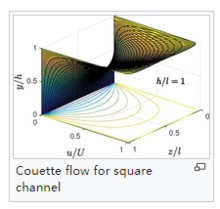，一维流u（y）是有效的。 当翼展方向长度为有限时，流量变为二维u（y，z）。 在流向方向上的无限长长度仍然需要保持，以确保流动的单向性质。3

下面考虑具有横向高度 h和翼展宽度 l的无限长的矩形通道，经受顶壁以恒定速度U移动的条件。无任何施加的压力梯度 ，Navier-Stokes方程减少到

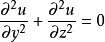边界条件为

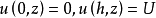
使用分离变量，解决方案为4

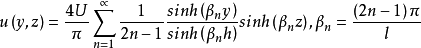
当h/l