定理定义
如果函数 在闭区间
在闭区间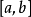 上连续,
上连续,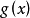 在
在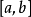 上不变号,并且
上不变号,并且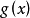 在闭区间
在闭区间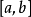 上是可积的,则在
上是可积的,则在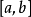 上至少存在一个点
上至少存在一个点 ,使下式成立:
,使下式成立:
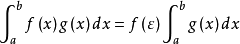
定理证明由于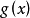 在
在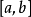 上不变号,不妨设
上不变号,不妨设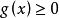 。并且由
。并且由 在
在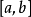 上的连续性可知,
上的连续性可知, 在
在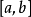 上存在最大值
上存在最大值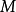 和最小值
和最小值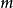 ,使得
,使得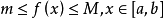 ,将不等式两边同时乘以
,将不等式两边同时乘以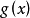 ,得到:
,得到:
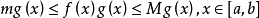
,对上式在上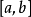 取积分得
取积分得
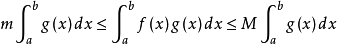
若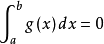 ,上式等号成立,
,上式等号成立,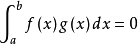 ,定理显然成立。
,定理显然成立。
若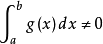 ,不等式两边同除以
,不等式两边同除以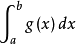 ,有
,有

由介值定理,存在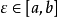 ,使得
,使得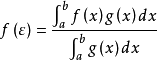 ,即
,即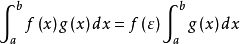 。定理得证。1
。定理得证。1
应用实例求极限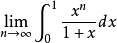 。
。
解:取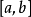 为
为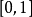 ,
,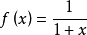 ,
,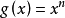 ,则
,则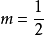 ,
, ,并有
,并有
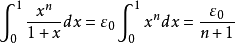
由于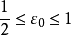 有界,因此
有界,因此
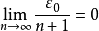 即原式的极限为0。2
即原式的极限为0。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国