[科普中国]-复合设计

基本介绍

设 是m个定量变量，它在一个试验域中变化，对任一变量 ，取定两个值 称为 的两个水平值，而值 称为 的中心值， 为 的试验 步长，一般在一个具体试验问题中，是带有量纲的数值，为了便于往后讨论，在此引进新的无量纲变量：

经过(1)的变换，中心点 变到新变量的坐标原点(0，0，…，0)，而各(因素)变量的两个水平值 变为1与-1。(1)的变换称为规格化变换，经过变换后的变量 称为标准化变量．在这本节中，所有变量都假定经过规格化变换的标准化变量。

所谓复合设计是一种对二次多项式模型

进行分批试验的一种设计。

因为（2）中共有 项组成，也就是说共有 个回归系数，要估计 个系数，至少要在 个不同点上试验．若试验布点任意，要估计 个回归系数，必须求解 阶线性方程组，计算工作量相当可观。能做到合理布点，使得能很简便地解出正规方程组呢?

设计步骤对模型(2)，G.E.P.Box.(1951)等提出一种较为合理的回归设计。这种设计把整个试验分成三批完成。

**第一批：**根据每个变量的±1两个水平值选用一张适当大小的二水平的完备型正交表，从中取出强度为4的m(≥4)个列，组成一张 型的试验方案表，表中2水平用 代替．在完成 表上的n个试验后，再做第二批试验。

**第二批：**在中心点(0， 0，...，0)作n0次重复试验，这批试验主要用来检验第一批的n个试验观察值的平均值 与第二批 中心点重复观察值的平均值 之间是否有显著差别。若无显著差别，则可停止试验，用 个试验观察值去估计线性回归方程

中的回归系数，其解为

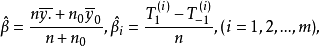其中 分别表示前n个试验中第i变量的1水平与一1水平的观察值之和，假若 与 之间有显著差别，这时应进行第三批试验。

第三批试验是在每个变量的坐标轴上，取臂长为 的两个对称点，m个变量共有2m个点，三批试验总共完成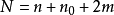 个试验，这N个试验点分布在以中心点为球心的两个同心球上，第一批试验分布在半径为 的球面上；第二批试验是在球心重复；第三批试验分布在半径为a的球面上。1