[科普中国]-正交多项式回归

正交多项式回归是用正交多项式表安排试验和回归分析处理数据。它与用最小二乘法配制的一般多项式回归不同，其回归系数的估计是互相独立的，若统计检验某一回归系数与零无显著性差异，只需从回归方程中删去这一项，而无需对其他的回归系数重新进行计算。

多项式回归虽然是一种有效的统计方法，但这种方法存在着两个缺点：一是计算量较大，特别是当自变量个数较多，或者自变量幂较高时，计算量迅速增加；二是回归系数间存在着相关性，从而剔除一个变量后还必须重新计算求出回归系数。

当自变量x的取值是等间隔时，可以利用正交性原理有效地克服上述缺点。这种多项式回归方法就是正交多项式回归。1

正交多项式对于定义在区间上[a,b]的一个函数系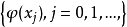 ，如果其中任何两个函数在此区间上的积分为零，而他们之中每个函数自乘的积分不等于零，即

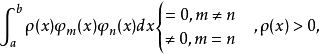则称此函数系为在此区间上关于权函数 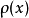的正交函数系。

当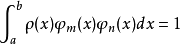 时称之为规范的正交函数系；当此函数系中每一个函数均为多项式时称之为正交多项式（系）。2

数学模型设变量y和x的n组观测数据服从以下k次多项式

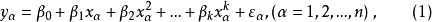令

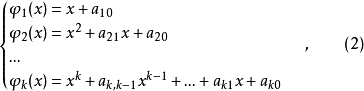
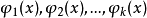分别是x的一次，二次,...,k次多项式， 是一些适当选择的常数，如何选择将在下面讨论(i=1,2,…，n)。将（2）式带入（1）式，则有

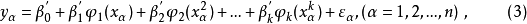比较（3）和（1）式可知，二者系数间存在简单的函数关系，只要求出 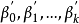，就可以求出 。

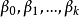若把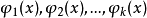 看作新的自变量，则(3)式就成为一个k元线性模型，其结构矩阵为

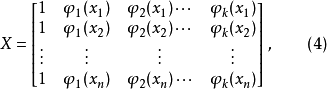正规方程为

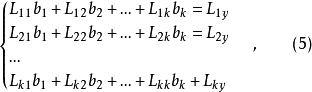
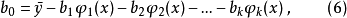其中

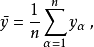
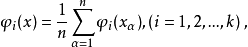
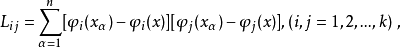
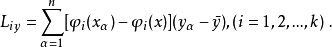
在多项式回归中遇到的困难是解正规方程系数矩阵的工作量太大，可以使其对角线上的元素不为零，而其余元素均为零，从而简化计算，而且同时消去了系数间的相关性。

对于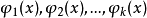 我们可以通过选择系数 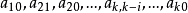使得

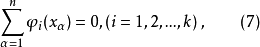
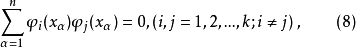从而使

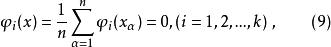
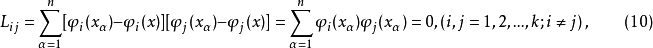
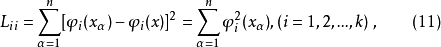
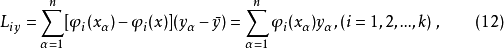则正规方程组为

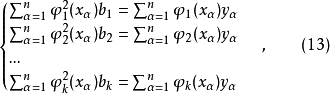回归系数为

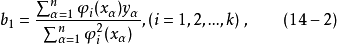满足(7)和(8)式的多项式组…我们称之为正交多项式。

在正交多项式回归中自变量的选择是等间隔的，设间隔为h,x0=a, 则

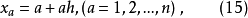若令

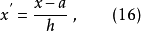则

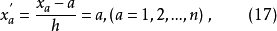
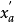是1至n的正整数。

为简化问题，用 代替x作为自变量。在条件许可时，取自变量x1=1,x2=2,…，xn=n。当x1=1,x2=2,…，xn=n时有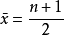 ，这时验证以下多项式是正交的，即

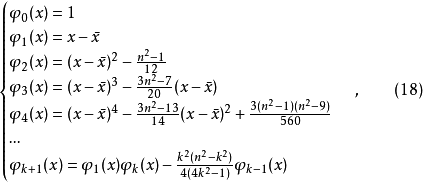显然，当x取正整数时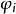， 不一定是整数，为了克服这给计算上带来的困难，取

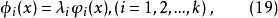
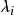使x取正整数时 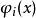是整数。可以验证用正交多项式 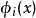代替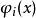 所求得的回归方程与用正交多项式 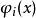所求得的回归方程是完全一样的。

对于正交多项式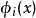 有

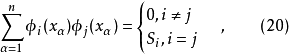不同的n相对应的 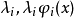在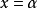 时的值以及Si值都已制成正交多项式表，根据正交多项式表，可以计算出回归方程的系数。令

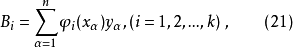则

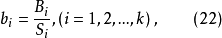回归方程为

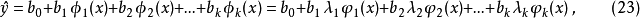由于正交多项式回归系数之间不存在相关性，因此某一项如果不显著，只要将它剔除即可，而不必对整个回归方程重新计算。1

回归系数的显著性检验正交多项式回归方程与回归系数的显著性检验可利用正交多项式的性质按表1进行。经检验不显著的高次项可以剔除，将其效应并入残差平方和，自由度也同时并入，如果对回归方程精度不满意，可以增加高次项，而已经计算出的结果不必重算。1

表1 正交多项式回归方差分析表

|| ||

程序框图1.数学模型：

2.变量及数组说明：

J－正确读入数据的控制变量；

N－试验组数；

M－所取正交多项式项数；

X(I)－存自变量数值；

Y(I)－存因变量数值；

Z(I)－存Y(I)的平方项；

E(I,1)－存在正交多项式一次项 ；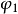

E(I,2)－存在正交多项式二次项 ；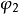

E(I,3)－存在正交多项式三次项 (其中I=1,…N)；

S(J)－结构矩阵逆矩阵元素 J=1,2,3；

B(J)－常数项矩阵B J=1,2,3；

D(J)－回归系数 J=0,1,2,3；

Q(J)－偏回归平方和 J=0,1,2,3；

S0－剩余平方和；

S－标准离差；

S1－总平方和；

F(J)－F检验值。

3.程序框图：

见如下图11

本词条内容贡献者为:

孙和军 - 副教授 - 南京理工大学