设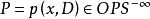 有标量主象征
有标量主象征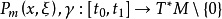 是
是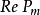 的零次特征带,在
的零次特征带,在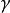 的邻域上
的邻域上 ;再设在
;再设在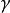 上,
上,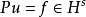 。如果在
。如果在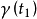 上,
上,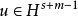 ,那么在
,那么在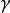 上,也有
上,也有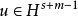 (对于
(对于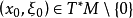 ,若记
,若记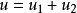 ,有
,有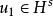 ,并且
,并且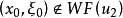 ,则称在
,则称在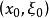 上
上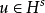 )。特别地,如果
)。特别地,如果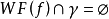 ,并且
,并且
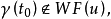 那么
那么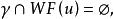 如果
如果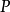 有实主象征,
有实主象征,
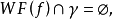 并且
并且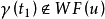 ,那么也有
,那么也有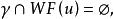 ,而且
,而且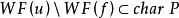 。此外,在哈密顿场
。此外,在哈密顿场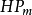 的作用下,
的作用下,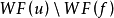 是不变的,也就是奇性沿着
是不变的,也就是奇性沿着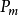 的零次特征带上传播1。
的零次特征带上传播1。
设p是一个给定的m阶偏微分算子,它的主象征为实值函数,则称
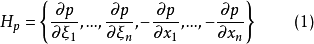 为
为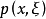 的Hamilton向量场,它的积分曲线为下面方程组
的Hamilton向量场,它的积分曲线为下面方程组
 的解,称为次特征带(或简称为次特征),显然,若
的解,称为次特征带(或简称为次特征),显然,若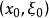 满足
满足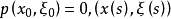 为过
为过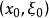 的次特征带,则由于
的次特征带,则由于
 故有
故有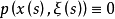 ,这样的次特征带称为零次特征带。
,这样的次特征带称为零次特征带。
下面叙述的算子p将满足条件:在p的特征集上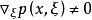 ,这样的算子称为主型算子(或称为狭义主型算子),由(2)知,对主型算子,在其次特征带上任一点均有
,这样的算子称为主型算子(或称为狭义主型算子),由(2)知,对主型算子,在其次特征带上任一点均有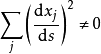 。
。
我们称次特征带在空间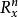 上的投影为次特征线。对于主型偏微分算子来说,它的次特征线不可能退化为一点2。
上的投影为次特征线。对于主型偏微分算子来说,它的次特征线不可能退化为一点2。
我们先考察一阶双曲型方程解的奇性传播定理,对于一阶线性偏微分方程,它的解容易直接求出,故解的奇性传播规律也不难得到。下面我们讨论一阶双曲型拟微分方程,它将成为对一般高阶方程解的奇性传播规律讨论的准备。
设P为一阶双曲型拟微分算子,它的主象征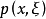 是
是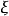 的正齐一次函数,由于
的正齐一次函数,由于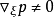 ,故不妨认为
,故不妨认为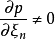 以下讨论的P的形式为
以下讨论的P的形式为
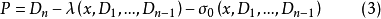 其中
其中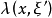 为齐一次实函数,
为齐一次实函数,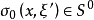 ,它可以写成为
,它可以写成为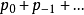 ,这里
,这里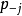 为
为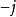 次函数有如下的命题:
次函数有如下的命题:
定理1 若P为(3)中定义的算子,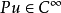 ,
,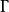 为
为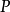 的零次特征带,
的零次特征带,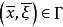 ,如果
,如果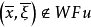 ,则整个
,则整个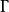 均不属于
均不属于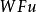 。
。
定理2 设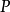 为m阶具
为m阶具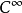 系数的偏微分算子,它的主象征
系数的偏微分算子,它的主象征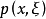 为实函数,且满足
为实函数,且满足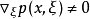 ,u为满足
,u为满足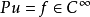 的解,如果
的解,如果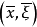 满足
满足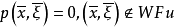 ,则过
,则过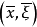 的零次特征带
的零次特征带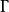 上任一点均不属于
上任一点均不属于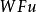 。2
。2




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国