常系数微分算子(differential operator with constant coefficients)是系数为常数的线性偏微分算子。赋范向量空间E的连续自同态通常叫做有界算子,或简称为算子。 定义在E的向量子空间上(该子空间在E中稠),而在E中取值的所有线性映射则叫做E的非有界算子。常系数微分算子是赋以一致收敛范数的R之区间[a,b]上的全体连续函数之向量空间的非有界算子。
基本介绍常系数微分算子是系数为常数的线性偏微分算子,其一般形式为:
 其中
其中 为常数(实数或复数)。例如,拉普拉斯算子
为常数(实数或复数)。例如,拉普拉斯算子
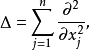 热算子
热算子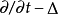 ,波算子
,波算子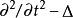 等都是常系数微分算子。线性偏微分算子理论中的若干重要问题,如基本解的存在性、局部可解性、亚椭圆性的判定等对于常系数情形均已完全解决1。
等都是常系数微分算子。线性偏微分算子理论中的若干重要问题,如基本解的存在性、局部可解性、亚椭圆性的判定等对于常系数情形均已完全解决1。
基本解的存在性定理基本解的存在性定理(theorem for existence offundamental solution)是关于基本解存在性的一个定理。该定理断言:每个非零的常系数微分算子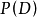 都有基本解,
都有基本解,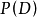 的基本解E作为广义函数可如下构造:
的基本解E作为广义函数可如下构造: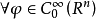 ,
,
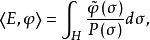 其中
其中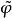 表示
表示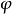 的逆傅里叶变换。H为
的逆傅里叶变换。H为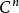 中某个适当的区域,满足
中某个适当的区域,满足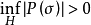 ,由基本解的存在可知常系数微分算子是局部可解算子。
,由基本解的存在可知常系数微分算子是局部可解算子。
亚椭圆常系数微分算子亚椭圆常系数微分算子(hypoelliptic differential operator with constant coefficients)是最基本的亚椭圆算子,设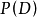 是常系数微分算子,则下述条件中的每一个都是
是常系数微分算子,则下述条件中的每一个都是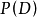 为亚椭圆算子的充分必要条件:
为亚椭圆算子的充分必要条件:
1.以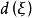 记
记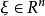 集合
集合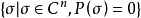 的距离,则当
的距离,则当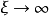 时,
时,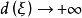 。
。
2.存在正的常数c及C,当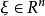 且
且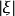 充分大时,不等式
充分大时,不等式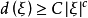 成立。
成立。
3.记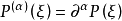 ,对于每个非零多重指标
,对于每个非零多重指标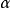 ,当
,当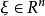 且
且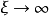 时,有
时,有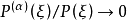 。
。
4.存在正的常数c及C,当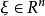 且
且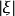 充分大时,不等式
充分大时,不等式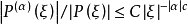 成立1。
成立1。
施瓦兹定理**施瓦兹定理[Schwarz(th.de)]**设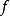 为
为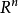 的开集
的开集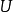 上的连续可微的数值函数,且在
上的连续可微的数值函数,且在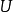 的点
的点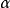 处两次可微,则对
处两次可微,则对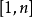 的任一相异元素偶
的任一相异元素偶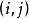 ,必有
,必有

这个定理表明,在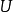 上无限可微的全体函数之向量空间
上无限可微的全体函数之向量空间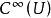 的全体自同态之代数中,所有自同态
的全体自同态之代数中,所有自同态
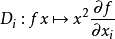 两两可交换。因此,由这些自同态生成的酉子代数是交换的;它的元素是常系数微分算子2。
两两可交换。因此,由这些自同态生成的酉子代数是交换的;它的元素是常系数微分算子2。
定强微分算子对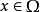 定义的微分算子称为在
定义的微分算子称为在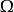 中具定强,若对任意固定的
中具定强,若对任意固定的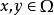 ,常系数微分算子
,常系数微分算子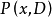 及
及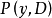 是等强的,即
是等强的,即
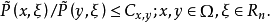 下面的引理把这个条件改成通常更方便的形式。
下面的引理把这个条件改成通常更方便的形式。
引理1 设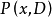 具定强,对固定的
具定强,对固定的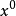 令
令 并设
并设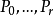 是弱于
是弱于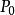 的常系数算子的有限维向量空间的基底,则有
的常系数算子的有限维向量空间的基底,则有
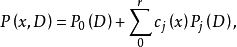 这里系数
这里系数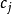 唯一确定,在
唯一确定,在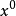 为0且有与
为0且有与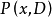 的系数相同的可微性及连续性质3。
的系数相同的可微性及连续性质3。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国