[科普中国]-二阶线性抛物型方程

二阶线性抛物型方程(linear parabolic equation of second order)是最重要的一类抛物型方程，全称是二阶线性抛物型偏微分方程。关于未知函数u(x1，x2，…，xn)的偏微分方程是一个含有u(x1，x2，…，xn)的偏导数的等式，其中最高阶偏导数的阶数称为该方程的阶。线性、非线性偏微分方程的意义与常微分方程相应的概念相类似。

基本介绍二阶线性抛物型方程是最重要的一类抛物型方程，对于二阶线性偏微分方程

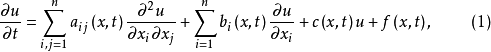式中系数和自由项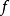均定义在柱体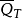上(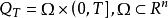)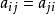，，如果矩阵(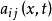)是正定的，即对任意实向量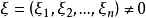， 有

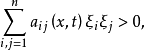则称方程(1)在点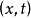是抛物的。如果方程(1)在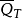上的一切点处都是抛物的，则称方程(1)在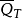上是抛物的。如果存在正常数ν和μ， 使对任意实向量ξ和一切点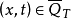都有

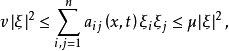则称方程(1)在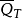上是一致抛物的。如果(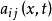)仅是非负定的，即对任意实向量ξ及某些点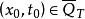，有

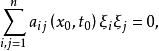则称方程(1)是退化抛物的。热传导方程

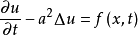是最简单的二阶线性抛物型方程1。

二阶线性抛物型方程的基本解二阶线性抛物型方程的基本解是二阶线性抛物型方程的一种具有奇性的特解，二阶线性抛物型方程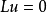在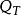中的基本解是一个对一切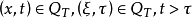都有定义的函数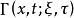，它满足如下条件：

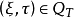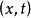1. 对固定的，作为的函数在域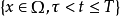中满足方程。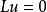

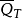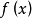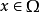2. 对每一个在上连续的函数，当时有

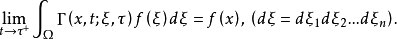热传导方程的基本解是

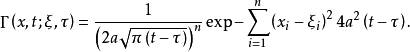
本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学