牛顿位势(Newton potential)是一般位势的经典模型之一。在Rn(n≥3)中,2核K=|x-y|2-n称为牛顿核,相应的位势称为牛顿位势。当n=3时,据牛顿万有引力公式,一个物体(或其质量分布)产生的引力场在任何一点x的位势等于∫B(1/|x-y|)σdv(y),这里B表示物体所占据的区域,dμ=σdv,σ表示密度,dv是体积元素;且为表达简明略去一个常数因子。当σ仅集中在某一曲面Γ时,关于dμ=σdS在Γ上积分就是单层位势;若同时把1/|x-y|改为它关于y在Γ的内法向导数(∂/∂n)(1/|x-y|),就得到所谓双层位势1。
基本介绍牛顿位势(Newtonian potential)是引力场的位势函数,对于区域Ω上一个可积函数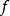 ,
,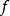 的牛顿位势是由下式定义的函数
的牛顿位势是由下式定义的函数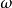
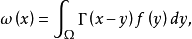 其中
其中
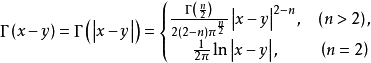 是拉普拉斯方程的基本解。当
是拉普拉斯方程的基本解。当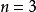 ,以
,以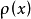 表示物体Ω的密度,
表示物体Ω的密度,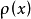 的牛顿位势为
的牛顿位势为
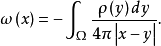 以k表示引力常数,由
以k表示引力常数,由
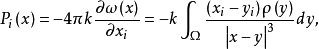 根据牛顿万有引力定律知道
根据牛顿万有引力定律知道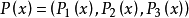 是物体Ω对点
是物体Ω对点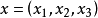 处单位质量的引力,而
处单位质量的引力,而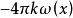 是引力
是引力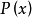 的位势。
的位势。
若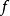 在Ω中有界可积,则f的牛顿位势
在Ω中有界可积,则f的牛顿位势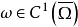 ,并且对任何
,并且对任何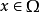 ,
,
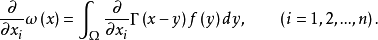 若
若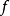 在Ω中有界且局部赫尔德连续,则
在Ω中有界且局部赫尔德连续,则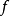 的牛顿位势
的牛顿位势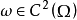 ,在Ω中
,在Ω中 ,并且对任何
,并且对任何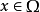 ,
,
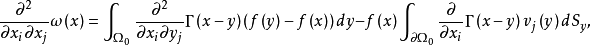
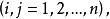 其中
其中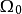 是任一包含Ω的区域,对于它,散度定理成立,并且
是任一包含Ω的区域,对于它,散度定理成立,并且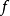 在Ω外延拓为零1。
在Ω外延拓为零1。
广义函数的牛顿位势广义函数的牛顿位势(Newton potential of distribution)是一类广义函数的位势,以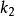 为广义函数核时
为广义函数核时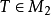 的位势
的位势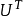 称为广义函数的牛顿位势,它是
称为广义函数的牛顿位势,它是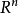 上的
上的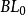 函数且
函数且
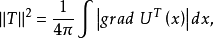 反之,任一
反之,任一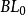 函数几乎处处等于某个牛顿位势
函数几乎处处等于某个牛顿位势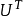 ,双层位势可视为
,双层位势可视为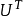 的特殊情形。
的特殊情形。
本词条内容贡献者为:
王海侠 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国