[科普中国]-二阶非线性双曲型方程

二阶非线性双曲型方程(second order nonlinear hyperbolic equation)是一类重要的二阶非线性方程。二阶双曲型方程的数值方法研究已有大量工作，如差分法、有限元法等，用差分法或有限元法进行数值计算，特别在处理多维问题时，需要解人型代数方程组。

基本介绍二阶非线性双曲型方程(second order nonlinear hyperbolic equation)是一类重要的二阶非线性方程，对于已解出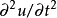的二阶非线性偏微分方程1

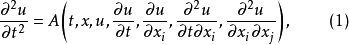
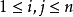，在函数A对变元

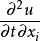和

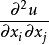的偏导数中视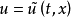为已知函数，并分别记为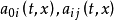，如果方程

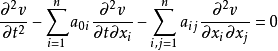是双曲型的，则称(1)在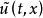的附近是双曲型的。

初值问题当考虑(1)的初值问题

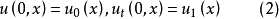时，如果函数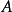是关于变元

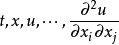的充分光滑函数且(1)在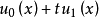的附近是双曲型的，则问题(1)，(2)在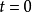的适当邻域中有惟一的解。一般地，非线性双曲型方程的初值问题只存在局部解1。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学