[科普中国]-蒙日方程

简介

在偏微分方程的数学理论中，以Gaspard Monge命名的蒙日方程是独立变量x1，...，xn中未知函数u的一阶偏微分方程。1

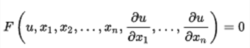
这是u的偏导数中的多项式。 任何蒙日方程都有一个蒙日锥。

通常，将u = x0，写入程度为k的蒙日方程式：

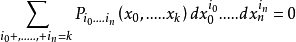
并表示差分dxk之间的关系。 给定点（x0，...，xn）上的蒙格锥是该点切线空间中的方程的零轨迹。

蒙日方程与（二阶）蒙日-安培方程无关。

蒙日锥（Monge cone）在偏微分方程（PDE）的数学理论中，蒙日锥是与一阶方程相关联的几何对象。2 它被命名为Gaspard Monge。 在两个方面，让

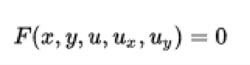
作为两个变量x和y中的未知实值函数u的PDE。 假设这个PDE是非退化的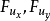，在定义域中既不为零， 修正一个点（x0，y0，z0）并考虑具有的解函数u

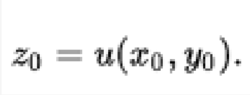
（1）满足（2）的每个解确定图形的切平面

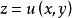
通过点（x0，y0，z0）。 随着对（ux，uy）求解（1）的变化，切平面包围在R3中具有顶点（x0，y0，z0）的圆锥，称为蒙日锥。 当F为准线性时，蒙日锥退化为称为蒙日轴的单线。 否则，蒙日锥体是一个适当的锥体，因为通过固定点的平面和非同轴单参数系列的平面包围锥体。 显然，原始偏微分方程在R3的余切束上产生一个标量值函数，在一个点（x，y，z）上由

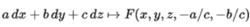
F的消失决定投影平面中具有均匀坐标（a：b：c）的曲线。 双曲线是该点的投影切线空间中的曲线，该曲线上的仿射锥是蒙日锥。 锥体可以具有多个分支，每个分支在投影切线空间中的简单闭合曲线上具有仿射锥。

当基点（x0，y0，z0）变化时，锥体也会变化。 因此，蒙格锥是R3上的锥形场。 因此，（1）的寻找解可以被解释为在该点处找到与蒙日锥相切的表面。 这是特征的方法。

该技术推广到n个空间变量中的标量一阶偏微分方程；即，

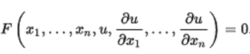
通过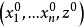，蒙日锥（或准线性情况下的轴）是PDE与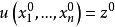。3