不变统计量(invariant statistic)是当对样本作某种变换时,其值保持不变的统计量。设G= {g}是样本空间到自身的某种一对一变换的全体(变换群)。称统计量T(X)= T (X1,…,Xn)关于G为不变统计量,如果对于任意变换g∈G和几乎 一切样本值x= (X1,…,Xn),有T(gx)=T(x),其中gx表示由样本点x经变换g所得新样本点(即x的象点)。如,对于加以常数g的推移变换g: gx= (x1+g,…,Xn+g),样本方差S2是不变统计量。称关于G的不变统计量为“最大不变统计量”,若任何关于G的不变统计量都是该统计量的函数。
基本介绍不变统计量(invariant statistic)是当对样本作某种变换时,其值保持不变的统计量。设G= {g}是样本空间到自身的某种一对一变换的全体(变换群)。称统计量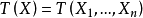 关于G为不变统计量,如果对于任意变换
关于G为不变统计量,如果对于任意变换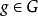 和几乎一切样本值
和几乎一切样本值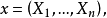 有
有
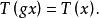
其中gx表示由样本点x经变换g所得新样本点(即x的象点)。如,对于加以常数g的推移变换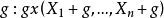 ,样本方差
,样本方差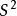 是不变统计量。称关于G的不变统计量为“最大不变统计量”,若任何关于G的不变统计量都是该统计量的函数。如,对推移变换,
是不变统计量。称关于G的不变统计量为“最大不变统计量”,若任何关于G的不变统计量都是该统计量的函数。如,对推移变换, 是最大不变统计量;对于正交变换,
是最大不变统计量;对于正交变换,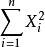 是最大不变统计量1。
是最大不变统计量1。
不变检验许多统计推断问题——参数估计和假设检验问题——本身呈现出某种不变性,此时要求使用的统计方法也应呈现出相应的不变性。
设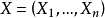 是从具有分布函数族
是从具有分布函数族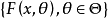 中抽取的一个简单随机子样,其中
中抽取的一个简单随机子样,其中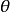 是未知参数,
是未知参数,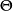 是参数空间,即容许假设。
是参数空间,即容许假设。
设G是一个不变变换群,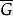 是G的导出变换群, 对于原假设
是G的导出变换群, 对于原假设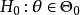 对备选假设
对备选假设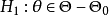 的检验问题,如果g的导出变换
的检验问题,如果g的导出变换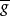 ,它既是
,它既是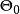 自身上的一一对应可逆变换,:也是
自身上的一一对应可逆变换,:也是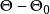 自身上的一一对应可逆变换,则称该检验阿题在g变换下保持不变。如果对每个
自身上的一一对应可逆变换,则称该检验阿题在g变换下保持不变。如果对每个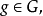 检验问题
检验问题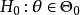 对
对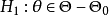 在g变换下保持不变,则称该检验问题在G 变换下保持不变2。
在g变换下保持不变,则称该检验问题在G 变换下保持不变2。
例1 设母体服从正态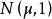 分布,
分布,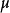 是未知参数,
是未知参数,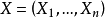 是取自该母体的一子样,考察检验问题:原假设
是取自该母体的一子样,考察检验问题:原假设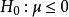 对备选假设
对备选假设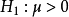 。
。
此例的容许假设是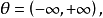 原假设
原假设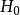 对应的子集是
对应的子集是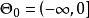 ,备选假设
,备选假设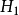 所对应的子集是
所对应的子集是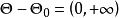 。
。
考察尺度变换群
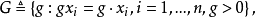 它的导出变换群是
它的导出变换群是
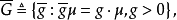 对任一
对任一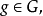 由于g>0,所以如果
由于g>0,所以如果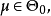 即
即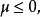 则
则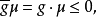 即
即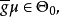 和
和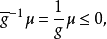 即
即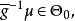 这证明了
这证明了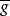 是
是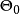 自身上的一一对应可逆变换,类似地可证明
自身上的一一对应可逆变换,类似地可证明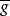 也是
也是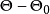 自身上的一一对应可逆变换,也就是说检验问题
自身上的一一对应可逆变换,也就是说检验问题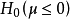 对
对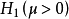 在g变换下保持不变。由g的任意性得到,该检验问题在尺度变换群G之下是不变的。
在g变换下保持不变。由g的任意性得到,该检验问题在尺度变换群G之下是不变的。
因为对于假设检验问题,仅采取两种可能的决策:接受 或拒绝
或拒绝 。因此对于在G变换下保持不变的检验问题,不变原理要求如果
。因此对于在G变换下保持不变的检验问题,不变原理要求如果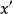 是变换
是变换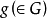 作用到原数据x上所得到的新数据
作用到原数据x上所得到的新数据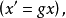 那末由
那末由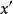 所作出的决策应和由x所作出的决策一致。也就是说,检验函数
所作出的决策应和由x所作出的决策一致。也就是说,检验函数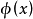 满足条件
满足条件
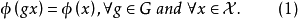 (实际上,上式仅要求对几乎所有的x成立)满足上式的检验
(实际上,上式仅要求对几乎所有的x成立)满足上式的检验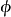 被称为是关于G不变的;简称为不变检验。
被称为是关于G不变的;简称为不变检验。
如果一个检验问题在某个变换群之下是不变的,此时不变原理要求致力于考虑不变检验,然后在不变检验类中寻找最优检验,对于许多检验问题,它不存在一致最优势检验,而可以在较小的不变检验类中存在一致最优势不变检验。因此不变性与无偏性相类似,它也是一种附加在检验法上的比较合理的限制。
为了寻找最优的不变检验,先考察不变检验的特征,由(1)式可以看到,在集合
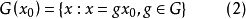 上,
上,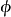 必保持常数。习惯上称由(2)式所定义的集合
必保持常数。习惯上称由(2)式所定义的集合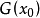 为
为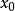 关于G 的迹。
关于G 的迹。
如果一个缆计量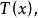 它在每个迹上保持常数,也就是说,
它在每个迹上保持常数,也就是说,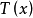 演足关系式
演足关系式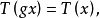 对一切
对一切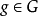 和几乎所有的
和几乎所有的 ,则称
,则称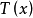 是关于G 的不变统计量,显然不变检验一定是不变统计量。
是关于G 的不变统计量,显然不变检验一定是不变统计量。
若一个不变统计量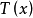 ,如果有
,如果有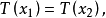 则存在
则存在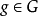 ,使得
,使得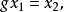 这样的
这样的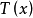 称为最大不变统计量。直观地说最大不变统计量在每个迹上保持常数,且在不同的迹上取不同的常数2。
称为最大不变统计量。直观地说最大不变统计量在每个迹上保持常数,且在不同的迹上取不同的常数2。
相关定理定理1 设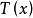 是关于G的最大不变统计量,则检验函数
是关于G的最大不变统计量,则检验函数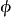 是不变检验的充要条件是存在函数h,使得
是不变检验的充要条件是存在函数h,使得
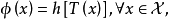 也就是说
也就是说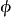 仅通过
仅通过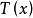 依赖于
依赖于 。
。
证明: 如果
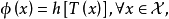 则
则
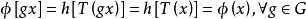 和
和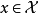 ,所以
,所以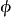 是不变检验。
是不变检验。
反之,如果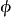 是不变的,且
是不变的,且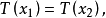 则由于T是最大不变的,因此一定存在g使得
则由于T是最大不变的,因此一定存在g使得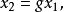 所以
所以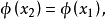 即
即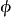 通过T依赖于x。
通过T依赖于x。
定理1的结论实际上对一切不变统计量都成立。
定理1指出,任何一一个不变检验都是最大不变统计量的函数,但是最大不变统计量仍很复杂,因此此时基于最大不变统计量寻找最优不变检验仍是困难的。最优检验可以在由充分统计所构造的检验类里去寻找。因此如果我们能够找到关于最大不变统计量的导出分布族的充分统计量,即最大不变充分统计量。那么最优不变检验就可以局限在由最大不变充分统计量所构造的检验类里去寻找。
如何寻找最大不变充分统计量呢? 按照常规的路径是先寻找最大不变统计量,及由最大不变统计的导出分布族,然后求出关于该导出分布族的充分统计,按此路径求最大不变充分统计量是困难的。Stein指出,在一定的条件下,最大不变充分统计量是关于充分统计的最大不变统计量,也就是说,此时我们可以先找出充分统计,然后对充分统计考察它在G 变换下的最大不变统计,通过这一路径寻找最大不变充分统计量往往比较方便2。
本词条内容贡献者为:
胡启洲 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国