[科普中国]-有界完全统计量

有界完全统计量(boundedly complete statistic)是常用的一类完全统计量，设(X，BX，P)是一个统计结构，其中P={Pθ：θ∈Θ}，如果对于BX可测的有界函数φ(X)，由ᗄθ∈Θ，有Eθφ(X)=0，可推出φ(X)=0，a.s. 对P中任一分布成立，则称此统计结构为**有界完全(备)**的，或称分布族P是有界完全(备)的，如果统计量t(X)的诱导统计结构(T，BT，PT)是有界完全的，则称统计量t(X)是有界完全统计量1。

定义设变量X的样本空间为分布族为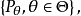为定义于取值于的统计量，其分布族为若对任何满足条件

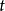的有界 可测函数，必有对一切，则称分布族为有界完全的.若为有界完全的，则称为有界完全统计量2。

相关结论及定理显然，完全的分布族或统计量必为有界完全的，下面的例子说明，此事实之逆不成立2。

例1设，分布族为

设对一切则

即

此式两边为的幂级数，在内收敛，故其对应项系数必相同，即

若要求有界，则由此知必须有，因而

这证明了为有界完全的。但它不为完全，因若取，当则易见对一切，但并不为1。

关于有界完全性有下面有趣的定理。

定理1 设X的样本空间和分布族为及，而为一有界完全统计量，取值于内，且为充分统计量，则对任何定义于的有限-可测函数，当的分布与无关时,对一切与独立。

值得注意的是: 本定理之逆不真。

由于指数族有完全(因而有界完全)和充分的统计量，故由以上定理得到:

系1 设X的分布族为指数族

而作为的子集有内点：则对任何(定义于且取值于某可测空间)，当的分布与无关时，对任何必与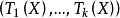独立(在这个具体情况下可以证明，上述事实之逆亦真)2。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学