[科普中国]-完全统计量

完全统计量（complete statistic）亦称完备统计量，是一类重要的统计量。由完全统计量的定义：E(g(S))=0对任意参数θ均成立时，即E=0对任意参数θ均成立，此时由T是完全统计量1。

背景统计量是统计理论中用来对数据进行分析、检验的变量。宏观量是大量微观量的统计平均值，具有统计平均的意义，对于单个微观粒子，宏观量是没有意义的．相对于微观量的统计平均性质的宏观量也叫统计量．需要指出的是，描写宏观世界的物理量例如速度、动能等实际上也可以说是宏观量，但宏观量并不都具有统计平均的性质，因而宏观量并不都是统计量．数理统计的基本概念。指不含未知参数的样本函数。如样本x1，x2，…，xn的算术平均数(样本均值)=1n(x1+x2+…+xn)就是一个统计量。从样本构造统计量，实际上是对样本所含总体的信息提炼加工；根据不同的推断要求，可以构造不同的统计量2。

在样本加工为统计量的过程中，样本中所含的信息可能有所损失，若在将样本加工为统计量时，信息毫无损失，则称此统计量为充分统计量。将样本加工成统计量要求越简单越好，最简单的充分统计量叫极小充分统计量。统计量的另一个重要的基本概念是完全统计量，完全充分统计量是极小充分统计量。

定义设（X1,...,Xn）的T次方为来自总体F（x；q）的一个样本，若统计量T=T（X1,X2,...,Xn）的分布族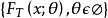是完备的分布函数族，则称T=T（X1,X2,...,Xn）为完全统计量3。

特征完全统计量的定义不如充分统计量那么明确，但由定义可见他有如下特征：

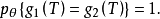
即T的分布函数是完备分布族。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学