[科普中国]-决策函数

简介

假设对一模式已抽取d个特征，表示为

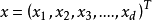
x是d维空间的一个向量。

模式识别问题就是根据模式的d个特征来判别模式属于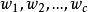 类中的哪一类。

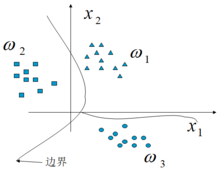
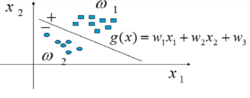
例如下图：三类的分类问题，它们的边界线就是一个决策函数。1

分类判决函数包含两类： 一类是线性判决函数，具体包括：

（1）线性判决函数

（2）广义线性判决函数（所谓广义线性判决函数就是把非线性判别函数映射到另外一个空间变成线性判决函数）

（3）分段线性判决函数

另一类是非线性判决函数。

我们现在对两类问题和多类问题分别进行讨论2。

(一)两类问题 即:：

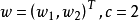
二维情况 ：取两个特征

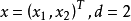
这种情况下，判决函数：

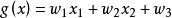
w为参数，x1,x2为坐标值。

在两类别情况，判决函数 g (x) 具有以下性质：

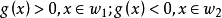
这时二维情况下判决由判决边界分类，情况如图：

现抽取d个特征为：

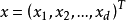
判决函数：

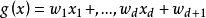
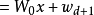
W0为权向量，x为模式向量。

模式分类：

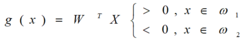
当 g1(x) =WTX=0 为判别边界 。当d=2时，二维情况的判别边界为一直线。当d=3时，判别边界为一平面，d>3时，则判别边界为一超平面。

(二)多类问题

对于多类问题，模式有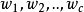 个类别。可分三种情况：

第一种情况：每一模式类与其它模式类间可用单个判决平面分开。这种情况，c类可有c个判别函数，且具有以下性质：

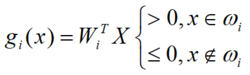
式中，Wi为第i个判别函数的权向量。

第一种情况

如下图所示，每一类别可用单个判别边界与其它类别相分开 。 如果一模式X属于ω1，则由图可清楚看出:这时g1(x) >0而g2(x)