[科普中国]-局部鞅

定义

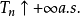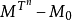设M为一右连续适应过程，称M为一局部鞅(相应地，局部上鞅，局部可积变差鞅)，如果存在停时 ，使得每个 为一致可积鞅(相应地，类(D)上鞅，可积变差鞅).

类似地，我们可以定义局部有界鞅、局部平方可积鞅等概念。

由定义我们可以看出以下事实：

1)局部鞅为一右连左极适应过程；

2)右连续鞅为局部鞅(令 )；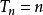

3)局部鞅空间为线性空间；

4)设M为局部鞅，T为停时，则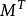 为局部鞅。2

基本性质性质1 设M为一非负局部上鞅，若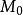 可积，则M为上鞅。2

性质2 设M为一右连续适应过程，

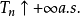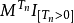1)为要M是局部鞅，必须且只需存在停时 ，使得每个 为一致可积鞅。

2)设S，T为两个停时，使得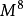 及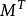 为一致可积鞅，则 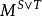也为一致可积鞅。

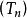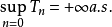3)如果存在停时列 ，使得 ，且每个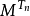 为局部鞅，则M为局部鞅。

性质3 设M为一局部鞅，T为一停时，则为要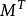为一致可积鞅，必须且只需 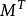为类(D)过程。

性质4 设M为一局部鞅，T为一停时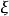， 为一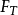 可测实值随机变量，则 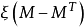为局部鞅。

性质5 可料局部鞅为连续局部鞅。2

性质6 设M为一可料的局部可积变差鞅，则。

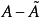性质7 设A为一局部可积变差适应过程， 为其可料对偶投影，则 为唯一的可料有限变差过程，使得 为零初值局部鞅。2

性质8 设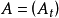 为一适应局部可积变差过程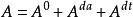， ，其中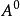 为A的连续部分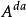， 为A的可及跳部分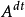， 为A的绝不可及跳部分，则

1)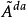 为纯断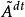的， 为连续的；

2)为要 连续，必须且只需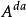 为局部鞅；

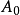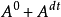3)为要 纯断。必须且只需 =0，且 为局部鞅。

性质9 设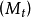 为一局部可积变差鞅,令

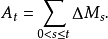
则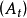 为一局部可积变差过程，且其可料对偶投影 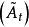连续．我们有

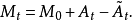
此外，若M只有可及跳，则

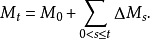
性质10 设X为一非负右连续上鞅，则X有如下唯一分解：2

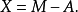
其中M为在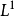 中有界的局部鞅，A为一零初值可料可积增过程。

基本定理与局鞅分解1．设M为一局部鞅，则对任给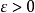 ，M可作如下分解：

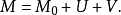
其中U为零初值局部有界鞅，且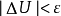；V为局部可积变差鞅，如果M拟左连续，则可要求U及V也拟左连续，且U与V无公共跳。

2. 有限变差局部鞅为局部可积变差鞅。2

3. 设A为一适应有限变差过程，则为要A为局部可积变差过程，必须且只需存在一可料有限变差过程B使得A 一B为局部鞅。2

4. 设M为一局部鞅，称M为纯断局部鞅，如果世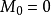，且M可作如下分解：

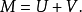
其中U为零初值局部纯断平方可积鞅，V为零初值有限变差局部鞅。2

5. 设M为一局部鞅，则M有如下唯一分解：

其中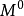为连续局部鞅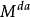，为只有可及跳的纯断局部鞅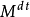，为只有绝不可及跳的纯断局部鞅。2