一过程(At)t∈R+称为增过程,如果它的所有轨道为R+上的非负有限值、右连续增函数,两个增过程之差称为有限****变差过程(process with finite variation)1。
定义有限变差过程是一类随机过程,指可以表为两个增过程之差的随机过程。设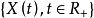 是一有限变差过程,把
是一有限变差过程,把
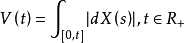 称为它的变差过程,其中积分意义是对每个固定的
称为它的变差过程,其中积分意义是对每个固定的 在勒贝格-斯蒂尔杰斯意义下的积分,称
在勒贝格-斯蒂尔杰斯意义下的积分,称 为可积变差过程,如果
为可积变差过程,如果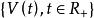 是可积的,这相当于
是可积的,这相当于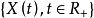 可表为两个可积增过程之差1。
可表为两个可积增过程之差1。
相关分析一过程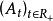 称为增过程,如果它的所有轨道为
称为增过程,如果它的所有轨道为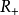 上的非负有限值、右连续增函数,两个增过程之差称为有限****变差过程。
上的非负有限值、右连续增函数,两个增过程之差称为有限****变差过程。
显然,有限变差过程为右连左极过程,从而适应有限变差过程为可选过程。此外,如果令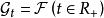 ,则一切有限变差过程都是关于
,则一切有限变差过程都是关于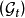 适应的。
适应的。
设A为一有限变差过程,我们约定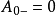 ,对一切
,对一切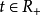 ,令
,令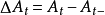 ,对
,对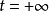 ,我们约定
,我们约定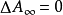 。
。
对每个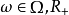 上的有限变差函数
上的有限变差函数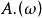 可以唯一地分解为:
可以唯一地分解为: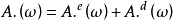 ,其中
,其中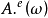 为连续有限变差函数,
为连续有限变差函数,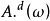 为纯断有限变差函数,我们有
为纯断有限变差函数,我们有
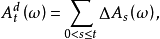 我们称过程
我们称过程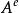 为A 的连续部分,称
为A 的连续部分,称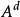 为A的纯断部分(或跳部分)。2
为A的纯断部分(或跳部分)。2
相关定理设A为一有限变差过程,称A为纯断的,如果 。
。
下一定理描绘了适应及可料有限变差过程的结构。
定理1 设A 为一适应(相应地,可料)有限变差过程,则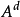 亦然(从而
亦然(从而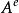 为可料)。此外,存在一列其图两两不相交的严格正停时(相应地,可料时)
为可料)。此外,存在一列其图两两不相交的严格正停时(相应地,可料时)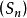 ,使得
,使得
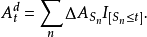
下一定理是前一定理的推论。
定理2 设A 为一纯断适应(相应地,可料)有限变差过程,则存在一列严格正停时(相应地,可料时)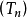 (这里,
(这里,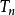 的图一般并非两两不相交),及一列实数
的图一般并非两两不相交),及一列实数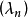 ,使得对一切
,使得对一切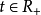 ,有
,有

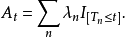 如果A为增过程,每个
如果A为增过程,每个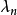 可取为正实数。
可取为正实数。
定理3 设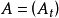 为一适应(相应地,可料)有限变差过程,则A的变差过程
为一适应(相应地,可料)有限变差过程,则A的变差过程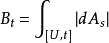 为适应(相应地,可料)增过程,且A可表为两个适应(相应地,可料)增过程之差。
为适应(相应地,可料)增过程,且A可表为两个适应(相应地,可料)增过程之差。
定义设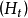 为一可测过程,
为一可测过程,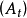 为一有限变差过程,如果对一切
为一有限变差过程,如果对一切 对一切
对一切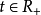 ,Lebesgue-Stieltjes积分
,Lebesgue-Stieltjes积分
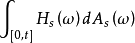 存在且有穷(即
存在且有穷(即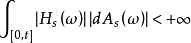 ,我们称
,我们称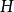 关于A可积,这时,令
关于A可积,这时,令
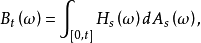 则
则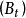 为有限变差过程,称
为有限变差过程,称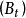 为H关于A的随机Stieltjes积分(或按轨道的Stieltjes积分,记为
为H关于A的随机Stieltjes积分(或按轨道的Stieltjes积分,记为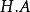 )。
)。
定理4设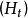 为一可测过程,
为一可测过程,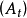 为一有限变差过程,且H关于A可积。
为一有限变差过程,且H关于A可积。
1) 如果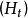 为循序的,且
为循序的,且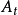 为适应的,则
为适应的,则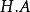 为适应的;
为适应的;
2) 如果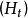 为可料的,且
为可料的,且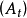 为可料的,则
为可料的,则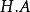 为可料的2。
为可料的2。
本词条内容贡献者为:
尚华娟 - 副教授 - 上海财经大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国