由一个图的全部顶点及连结这些顶点的部分边构成的连通图称为原图的支撑子图。给定连通图 ,若
,若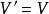 ,
,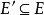 ,则称图
,则称图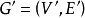 是由
是由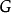 生成的部分图,记为
生成的部分图,记为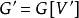 ,而当
,而当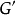 是连通的(任意两个顶点之间至少有一通路连接),称
是连通的(任意两个顶点之间至少有一通路连接),称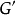 是
是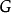 的支撑子图1。也即连通图
的支撑子图1。也即连通图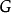 的支撑子图
的支撑子图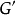 包含
包含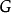 的所有顶点,并且是连通的2。
的所有顶点,并且是连通的2。
给定一个无向图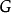 ,若
,若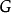 的一个支撑子图
的一个支撑子图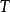 是树,则称
是树,则称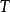 为
为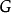 的支撑树。图的支撑树不是唯一的。但任何连通图至少有一颗支撑树。所有支撑树中具有最小数的支撑树称为最小支撑树,求最小支撑树是实际问题的需要,例如“为了把若干城市连接起来,设计最短通信线路”,“为了解决若干居民点供水,要求设计最短的自来水管线路”等等3。
的支撑树。图的支撑树不是唯一的。但任何连通图至少有一颗支撑树。所有支撑树中具有最小数的支撑树称为最小支撑树,求最小支撑树是实际问题的需要,例如“为了把若干城市连接起来,设计最短通信线路”,“为了解决若干居民点供水,要求设计最短的自来水管线路”等等3。
定义1 设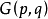 为
为 个顶和
个顶和 个边的任意连通图,则
个边的任意连通图,则 中任意
中任意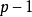 个边所导出的
个边所导出的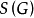 个子图称为支撑子图。
个子图称为支撑子图。
定义2 设图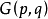 中存在
中存在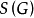 个支撑子图,则
个支撑子图,则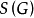 个支撑子图中
个支撑子图中 个不含圈的支撑子图称为支撑树,
个不含圈的支撑子图称为支撑树, 个含圈的支撑子图称为含圈的支撑子图,并有
个含圈的支撑子图称为含圈的支撑子图,并有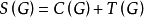 。
。
定理1 设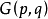 为任意连通图,则
为任意连通图,则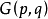 中任意
中任意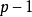 个边所导出的支撑子图的个数为
个边所导出的支撑子图的个数为
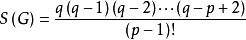
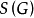 个支撑子图中含圈的支撑子图的个数为
个支撑子图中含圈的支撑子图的个数为
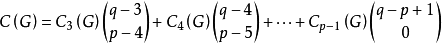
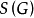 个支撑子图中不含圈的支撑子图(支撑树)的个数为
个支撑子图中不含圈的支撑子图(支撑树)的个数为
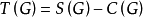
式中: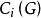 为图
为图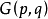 中
中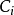 的个数;
的个数;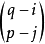 为
为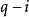 个边中任取
个边中任取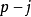 个边的选择数。
个边的选择数。
证明:不失一般性,设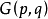 为
为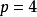 ,
,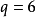 的完全图
的完全图 ,且
,且 中
中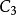 的个数
的个数 ;
;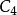 的个数
的个数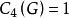 ,若定理1为真,则
,若定理1为真,则 中
中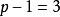 个边所导出的支撑子图的个数
个边所导出的支撑子图的个数
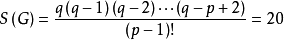
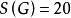 个支撑子图中含圈的支撑子图仅与圈
个支撑子图中含圈的支撑子图仅与圈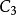 有关系,故含圈的支撑子图的个数为
有关系,故含圈的支撑子图的个数为
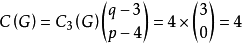
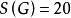 个支撑子图中不含圈的生成树的个数为
个支撑子图中不含圈的生成树的个数为
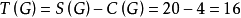
定理1得证3。
定理2及证明定理2 设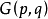 为任意连通图,则
为任意连通图,则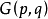 中
中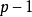 个边所导出的
个边所导出的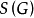 个支撑子图的构造归结为
个支撑子图的构造归结为
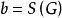 ,
,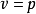 ,
,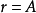 ,
,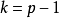 ,
,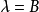 的
的 设计中
设计中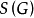 个区组的构造。由于
个区组的构造。由于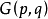 中
中 个边的编号为区组的变元,
个边的编号为区组的变元,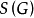 个支撑子图与
个支撑子图与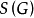 个区组一一对应,
个区组一一对应,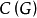 个含圈的支撑子图与
个含圈的支撑子图与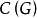 个区组一一对应,
个区组一一对应,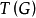 个支撑树与
个支撑树与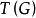 个区组一一对应,且有
个区组一一对应,且有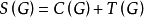 。
。
证明:不失一般性,设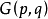 为
为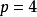 ,
,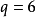 的完全图
的完全图 ,若定理2为真,则完全图
,若定理2为真,则完全图 的
的 个生成子图的构造归结为
个生成子图的构造归结为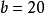 ,
,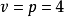 ,
,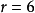 ,
,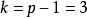 ,
,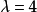 的
的 设计中下列20个区组:
设计中下列20个区组: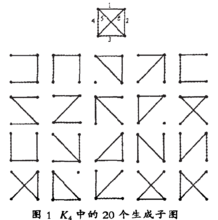
(1,2,3),(1,2,4),(1,2,5),(1,2,6),(1,3,4),(1,3,5),(1,3,6),(1,4,5),(1,4,6),(1,5,6),(2,3,4),(2,3,5),(2,3,6),(2,4,5),(2,4,6),(2,5,6),(3,4,5),(3,4,6),(3,5,6),(4,5,6)的构造,当中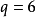 个边的编号被确定后,
个边的编号被确定后,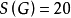 个支撑子图与20个区组一一对应,20个支撑子图中有4个含圈的支撑子图,有16个不含圈的支撑子图(支撑树)。亦即:
个支撑子图与20个区组一一对应,20个支撑子图中有4个含圈的支撑子图,有16个不含圈的支撑子图(支撑树)。亦即: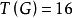 ,
,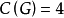 且
且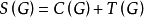 ,见图1。
,见图1。
定理2得证3。




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国