在Brelot调和空间(X,H)中,设G为开集,则称H(G)中的函数为G上的调和函数。对G上的下半连续函数u,若G中每一点x有一个开邻域Vx,使得对任何一个闭包包含于Vx的正则区域D恒有μDu≤u在D成立,则称u在G上(相对于H)是局部超调和的。用UH(G)表示G上所有相对于H是局部超调和的函数全体,则容易看到,对所有开集都作同样考虑得到的函数簇UH是X上的一个超调和簇且当记U'=UH时有HU'=H1。
基本介绍局部超调和函数(locally hyperharmonic function)是指在每一点的某个邻域上有超调和性的函数。设U是一个开集,u是U上的取值于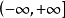 的下半连续函数,如果对每一
的下半连续函数,如果对每一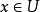 ,存在
,存在 的开邻域
的开邻域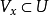 ,使得对任何满足
,使得对任何满足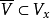 的正则区域
的正则区域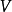 ,在
,在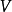 上恒有
上恒有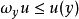 (
(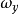 是V的U调和测度),那么u称为U上的(相对于H的)局部超调和函数,记
是V的U调和测度),那么u称为U上的(相对于H的)局部超调和函数,记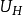 为U上的局部超调和函数全体,则
为U上的局部超调和函数全体,则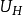 是X上的超调和簇,称为由H产生的超调和簇,并且,H就是与
是X上的超调和簇,称为由H产生的超调和簇,并且,H就是与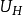 相关的调和簇2。
相关的调和簇2。
相关定理引理1 设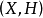 是Brelot调和空间,G为区域且
是Brelot调和空间,G为区域且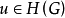 ,若u在G是正的(即
,若u在G是正的(即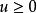 )且有
)且有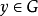 使得
使得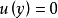 ,则u在G上恒等于01。
,则u在G上恒等于01。
证明: 设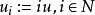 ,则
,则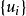 为
为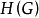 中的单调增加列,因为
中的单调增加列,因为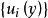 有界(实际上,每个
有界(实际上,每个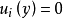 ),由公理3知
),由公理3知
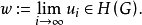 故对G中的x都有
故对G中的x都有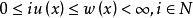 ;所以
;所以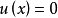 。
。
引理2 设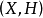 是Brelot调和空间,D是一个正则区域,W是一个开集使得
是Brelot调和空间,D是一个正则区域,W是一个开集使得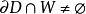 .那么对D中每个x成立
.那么对D中每个x成立

引理3 设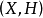 是Brelot调和空间,D是X的一个区域,
是Brelot调和空间,D是X的一个区域,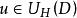 。若u在D的一个非空开子集W上恒等于
。若u在D的一个非空开子集W上恒等于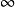 ,则它在D上也恒等于
,则它在D上也恒等于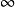 .换言之,u在D要么恒等于
.换言之,u在D要么恒等于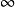 ,要么在D的一个稠密子集恒等于
,要么在D的一个稠密子集恒等于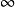 。
。
**证****明:**设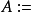 {
{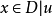 在x的一个开邻域上恒等于
在x的一个开邻域上恒等于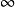 },显然A是包含W的开集,我们断言A=D,否则,设G是A的一个连通分支,于是
},显然A是包含W的开集,我们断言A=D,否则,设G是A的一个连通分支,于是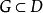 且
且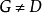 .因D是连通的,
.因D是连通的,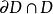 非空,设
非空,设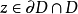 .因
.因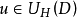 ,由局部超调和函数的定义,存在z的一个开邻域V,使得对任何一个闭包包含在V的正则区域U都有
,由局部超调和函数的定义,存在z的一个开邻域V,使得对任何一个闭包包含在V的正则区域U都有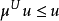 ,取定一个
,取定一个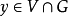 及一个正则区域U使得
及一个正则区域U使得 且U的闭包包含在
且U的闭包包含在 .因为G是连通的,故
.因为G是连通的,故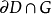 非空。由于u在
非空。由于u在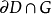 上恒等于
上恒等于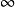 ,据上一引理知:对任意
,据上一引理知:对任意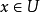 有
有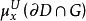 ;故
;故
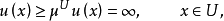 这说明
这说明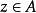 ,与z的定义矛盾,故
,与z的定义矛盾,故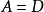 。
。
定理4 设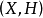 是Brelot调和空间,D是X的一个区域,
是Brelot调和空间,D是X的一个区域,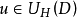 且在D上有
且在D上有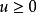 ,若存在D中的点z使得
,若存在D中的点z使得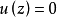 ,则
,则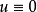 。
。
**证明:**令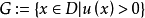 ,则G为开集,若G非空,令
,则G为开集,若G非空,令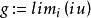 ,显然,
,显然,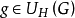 .因为在G上
.因为在G上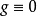 。由上一引理知,在D上也有
。由上一引理知,在D上也有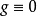 ,这表明对任意
,这表明对任意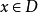 有
有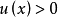 。
。
定理5 设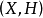 是Brelot调和空间,G是开集,若存在
是Brelot调和空间,G是开集,若存在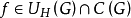 使得
使得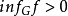 ,则G是相对于
,则G是相对于 的一个MP集。
的一个MP集。
定理6 若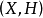 是Brelot调和空间,则
是Brelot调和空间,则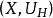 是一个
是一个 调和空间,而且每个局部超调和函数都是超调和函数,即:若G是开集,
调和空间,而且每个局部超调和函数都是超调和函数,即:若G是开集,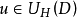 ,则在任何一个其闭包包含于G的正则区域D上有
,则在任何一个其闭包包含于G的正则区域D上有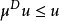 。
。
(关于文中所有结论的详细证明请参考相应书籍1)。
本词条内容贡献者为:
孙和军 - 副教授 - 南京理工大学




 扫码下载APP
扫码下载APP

 科普中国APP
科普中国APP
 科普中国
科普中国
 科普中国
科普中国