[科普中国]-绍凯表现定理

绍凯表现定理（Choquet representation theorem）是对应于马丁积分表现的一个著名的泛函分析定理。

简介绍凯表现定理是对应于马丁积分表现的一个著名的泛函分析定理。

绍凯表现定理的要点是：在一个局部凸的豪斯多夫拓扑线性空间Ω中，若凸锥C的底（即C与一个不经过原点的闭超平面之交）B为紧且可度量化，则B中每个元素y必是某个集中在B的极端点集上的概率测度μ的重心，即对Ω上任何连续的线性形式l，有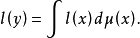

进一步，若凸锥C关于其自身的次序成为格，则上述表达式惟一这个定理及有关的研究被誉为20世纪中叶分析学上伟大发现之一。1

泛函分析泛函分析是20世纪30年代形成的数学分科，是从变分问题，积分方程和理论物理的研究中发展起来的。它综合运用函数论，几何学，现代数学的观点来研究无限维向量空间上的泛函，算子和极限理论。它可以看作无限维向量空间的解析几何及数学分析。

泛函分析在数学物理方程，概率论，计算数学等分科中都有应用，也是研究具有无限个自由度的物理系统的数学工具。

凸锥类特殊的凸集被称之为凸锥，它有极其重要的性质和应用。

既是锥又是凸集的点集称之为凸锥。常见的凸锥包括：二维平面中的半射线、整个n维欧式空间等。凸锥中有一个重要的定理，凸锥分离定理。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所