[科普中国]-广义马丁边界

广义马丁边界(generalized Martin boundaries )是马丁紧致化的推广形式的理想边界。马丁是美国数学家。生于阿肯色(Arkansas)斯普林代尔 (Springdale)，1930年毕业于阿肯色大学，1934年获伊利诺伊大学博士学位。

概念广义马丁边界(generalized Martin boundaries )是马丁紧致化的推广形式的理想边界。它有许多种，例如，用某个二阶椭圆型方程在Ω的格林函数G′(x，y)代替调和方程的G(x，y)，就得到与该方程某族极小正解相关联的马丁边界Δ′(称为椭圆马丁边界)及极小点全体Δ1′，并可研究Ω∪Δ′上的位势论性质以及方程的解空间结构；Δ′与Δ及其他理想边界的关系等是常见课题。特别地，对方程Lu=Pu(P≥0，L是拉普拉斯算子)， 把Δ1′的基数称为椭圆维数，记为dimP。中井三留(Nakai，M.)等日本学者在具有一个孤立边界点的平面区域上对dimP的值域与密度P的关系做了深入研究；另外，对非椭圆方程也可考虑广义马丁边界。

马丁空间马丁空间是位势论中的一类重要空间。格林空间Ω相对于函数族{Ky(x)|y∈Ω}的紧致化记为Ω^，并称Ω^为马丁空间，其中

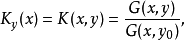y0∈Ω任意取定。Δ=Ω^\Ω称为马丁边界，每个函数Ky(x)在Ω^有连续延拓且能分辨Δ;Ω^可度量化。R的一般区域的欧氏边界与Δ全然不同，但当Ω是球或其他较为正则的域(如李普希茨域)时二者一致。对R的单连通格林区域， Δ等同于卡拉西奥多里(Carathéodory，C.)的分歧边界。对马丁边界同样可考虑狄利克雷问题；可把Ω上的细拓扑延拓成Ω∪Δ1上的极小细拓扑并可讨论函数的边界值问题；马丁边界可翻译成概率语言并在随机过程论中得到应用和推广。该空间是马丁(Martin，R.S.)于1941年引进的。1

位势论现代分析数学领域的一个分支，主要研究各种形式的位势(函数)和与其密切关联的调和函数、上(下、超、次)调和函数族的各种性质及其应用。经典位势论的主要研究工具是微积分，并与微分方程、复变函数论紧密关联；现代位势论以拓扑、泛函分析与测度论、广义函数等为主要工具，与分析数学领域的诸多分支相互渗透并和随机过程建立了深刻的内在联系。位势论起源于物理学的万有引力学说和静电学，远在1733年，拉格朗日(Lagrange，J.-L.)就注意到引力场是一个函数(称为牛顿位势)的梯度。

从20世纪40年代起，泛函分析、拓扑学的方法被系统地引入位势论并使它发展到一个新水平。1941年，嘉当(Cartan，H.)利用希尔伯特空间理论研究具有有限能量的测度等，得到很大成功；同年，马丁(Martin，R.S.)建立了马丁边界理论，导致了关于一般理想边界的深入研究；1950年，戴尼(Deny，J.)用广义函数论解决了完备化问题;1955年，绍凯(Choquet，G.)建立了一般容量理论及可容性定理，并用凸锥极端点理论改进了马丁的成果。此外，对于更一般空间(例如流形、LCA群)和更一般位势核的位势论也有了深入的探讨。

近30多年来，位势论迅速发展，其显著特点之一是各种公理体系的建立。为统一处理已有的理论并加以推广使之适用于一般椭圆型和抛物型方程或随机过程，自20世纪50年代中期起，陶茨(Tautz，G.)、杜布(Doob，J.L.)、布雷洛、鲍尔(Bauer，H.)、邦尼(Bony，J.M.)、康斯坦丁斯库(Constantinescu，C.)和柯尼(Cornea，A.)等人分别提出了不同的公理系统，建立各种形式的调和空间位势论(最近，关于多重调和空间及非线性位势论的公理系统也先后建立起来);而戴尼和博灵(Beurling，A.)等人则从能量和狄利克雷积分等概念出发建立了狄利克雷空间论。位势论发展的另一个显著特点是，越来越广泛深入地与相邻分支，如复分析(包括黎曼曲面)、拓扑学、几何测度论、微分几何、微分方程、调和分析等相互结合和渗透，且发挥日益明显的作用与影响。特别引人注目的是，对于它与随机过程论之深刻联系的深入研究，同时促进了这两个分支的繁荣和发展，在杜布、亨特(Hunt，G.A.)、迈耶(Meyer，P.A.)和钟开莱等人出色工作的基础上，产生了所谓概率位势论或马尔可夫过程位势论，与此有关的课题正吸引着大批学者去做深入研究。1

人物简介马丁是美国数学家。生于阿肯色(Arkansas)斯普林代尔 (Springdale)，1930年毕业于阿肯色大学，1934年获伊利诺伊大学博士学位。1936年以后，在马萨诸塞理工学院任教。曾还任美国数学协会副主席，美国科学艺术研究院院士。马丁的主要贡献在拓扑学方面，他建立了关于拓扑空间性质的马丁公理。在拓扑流形中有马丁-博特定理。专著有《多复变量函数》(1948，合著)、《函数空间的分析》(1964，合著)等。

本词条内容贡献者为:

尚华娟 - 副教授 - 上海财经大学