[科普中国]-非切向边界值

非切向边界值是区域上的函数当限制自变量以某种特殊方式趋近于边界点时的极限。

简介概述非切向边界值是区域上的函数当限制自变量以某种特殊方式趋近于边界点时的极限。

具体内容设D⊂Rn(n≥2)是一个李普希茨区域，即D为有界域且满足条件：对每点Q∈∂D，对应一个局部坐标系(X,y)，X∈Rn-1，y∈R1，及一个邻域N和函数b(X)，使得：

1、|b(X)-b(X')|≤k|X-X'|（k为常数）；

2、N∩D=N∩{(X,y)|y≥b(X)}；

3、N∩∂D=N∩{(X,y)|y=b(X)}。

设f是D上定义的函数，如果当x沿着任何一个以x0∈∂D为顶点的内锥Γ（即存在一个以x0为顶点的锥Γ'使得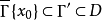 ）趋于x0时，f(x)有同一个极限值，就称f在x0有非切向边界值（角极限）。1

极限“极限”是数学中的分支——微积分的基础概念，广义的“极限”是指“无限靠近而永远不能到达”的意思。

数学中的“极限”指：某一个函数中的某一个变量，此变量在变大（或者变小）的永远变化的过程中，逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”（“永远不能够等于A，但是取等于A‘已经足够取得高精度计算结果）的过程中，此变量的变化，被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”（当然也可以用其他符号表示）。

本词条内容贡献者为:

杜强 - 高级工程师 - 中国科学院工程热物理研究所